题目内容
16.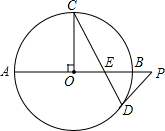 如图,AB是⊙O的直径,半径OC⊥AB,P是AB延长线上一点,PD切⊙O于点D,CD交AB于点E,判断△PDE的形状,并说明理由.
如图,AB是⊙O的直径,半径OC⊥AB,P是AB延长线上一点,PD切⊙O于点D,CD交AB于点E,判断△PDE的形状,并说明理由.
分析 连接OD,根据切线的性质得出∠ODP=90°,根据OC⊥AB,得∠CEO+∠OCE=90°,根据对顶角相等得出∠OEC=∠PDE,从而得出∠PDE=∠PED,判断△PDE的形状.
解答  解:△PDE是等腰三角形.
解:△PDE是等腰三角形.
理由是:连接OD,
∵OC⊥AB,
∴∠CEO+∠OCE=90°,
∵OC=OD,
∴∠OCE=∠ODE,
∵PD切⊙O,
∴∠ODE+∠PDE=90°,
∵∠OEC=∠PED,
∴∠PDE=∠PED,
∴PD=PE,
∴△PDE是等腰三角形.
点评 本题考查了切线的性质,等腰三角形的性质和判定,以及对顶角相等,常作的辅助线是连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.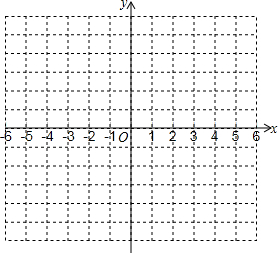 已知二次函数y=-x2+2x+2,
已知二次函数y=-x2+2x+2,
(1)用配方法把化为y=a(x+m)2+k的形式;
(2)选取适当的数据填入表,并在所给的直角坐标系内描点画出该抛物线的图象;
(3)若该抛物线上两点A(x1,y1),B(x2,y2)的横坐标满足x1>x2>1,根据图象可知y1<y2.(填“<”或“>”)
 已知二次函数y=-x2+2x+2,
已知二次函数y=-x2+2x+2,(1)用配方法把化为y=a(x+m)2+k的形式;
(2)选取适当的数据填入表,并在所给的直角坐标系内描点画出该抛物线的图象;
| x | … | … | |||||
| y | … | … |
5.一元二次方程x2-2x+3=0的根的情况是( )
| A. | 有两个相等的实根 | B. | 有两个不相等的实根 | ||
| C. | 无实数根 | D. | 有一个根 |
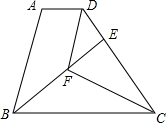 已知,如图,在梯形ABCD中,AD∥BC,BC=CD,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.
已知,如图,在梯形ABCD中,AD∥BC,BC=CD,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.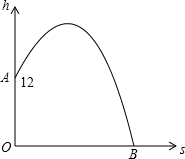 家在四楼的小明从窗口A向楼外掷出一个纸飞机,如果纸飞机下落过程值距离地面的高度h(米)与飞机的水平距离s(米)之间的关系式是h=-$\frac{1}{20}$s2+$\frac{2}{5}$s+m,其图象如图所示,那么这架纸飞机落地处点B与小明家所住的楼的相距20米.
家在四楼的小明从窗口A向楼外掷出一个纸飞机,如果纸飞机下落过程值距离地面的高度h(米)与飞机的水平距离s(米)之间的关系式是h=-$\frac{1}{20}$s2+$\frac{2}{5}$s+m,其图象如图所示,那么这架纸飞机落地处点B与小明家所住的楼的相距20米. 用8m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长,宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?
用8m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长,宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?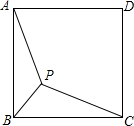 如图,已知点P是正方形ABCD内的一点,连结PA、PB、PC.若PA=4,PB=2,∠APB=135°,则PC的长为2$\sqrt{6}$.
如图,已知点P是正方形ABCD内的一点,连结PA、PB、PC.若PA=4,PB=2,∠APB=135°,则PC的长为2$\sqrt{6}$.