题目内容
19.某企业信息部进行市场凋研发现:信息一:如果单独投资A种产品.则所获利润 yA(万元)与投资金额x(万元)之间存在正比例函数关系:yA=kx,并且当投资5万元时.可获利润2万元.
信息二:如果单独投资B种产品.则所获利润yB(万元)与投资金额x(万元)之间存在二次函数关系:yB=ax2+bx.并且当投资2万元时.可获利润2.4万元;当投资4万元时,可获利润3.2万元.
(1)请分别求出上述正比例函数表达式与二次函数表达式;
(2)若该企业同时投资A种产品7万元,B种产品3万元,这样能获得的利润是多少?
分析 (1)根据所给数据易得方程和方程组,解之得函数表达式;
(2)根据(1)的函数表达式代入xA=7,xB=3求出利润和即可.
解答 解:(1)∵当x=5时,yA=2,
∴2=5k,
∴k=0.4.
∴yA=0.4x.
由yB=ax2+bx,
当x=2时,yB=2.4;
当x=4时,yB=3.2
∴$\left\{\begin{array}{l}{2.4=4a+2b}\\{3.2=16a+4b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-0.2}\\{b=1.6}\end{array}\right.$.
∴yB=-0.2x2+1.6x.
(2)当x=7时,yA=0.4×7=2.8.
当x=3时,yB=-0.2×32+1.6×3=3
故该企业同时投资A种产品7万元,B种产品3万元,这样能获得的利润是5.8万元.
点评 本题考查了运用待定系数法求一次函数、二次函数的解析式的运用,求出函数的解析式是解决问题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
9.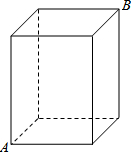 一个长方体盒子的长、宽、高分别为3cm,3cm,5cm,一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点B,蚂蚁爬行的最短路程是( )
一个长方体盒子的长、宽、高分别为3cm,3cm,5cm,一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点B,蚂蚁爬行的最短路程是( )
 一个长方体盒子的长、宽、高分别为3cm,3cm,5cm,一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点B,蚂蚁爬行的最短路程是( )
一个长方体盒子的长、宽、高分别为3cm,3cm,5cm,一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点B,蚂蚁爬行的最短路程是( )| A. | $\sqrt{73}$cn | B. | $\sqrt{61}$cm | C. | 3$\sqrt{6}$cm | D. | $\sqrt{53}$cm |
7.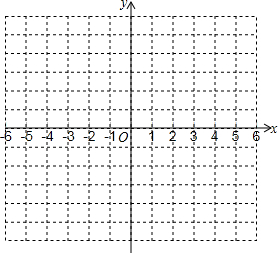 已知二次函数y=-x2+2x+2,
已知二次函数y=-x2+2x+2,
(1)用配方法把化为y=a(x+m)2+k的形式;
(2)选取适当的数据填入表,并在所给的直角坐标系内描点画出该抛物线的图象;
(3)若该抛物线上两点A(x1,y1),B(x2,y2)的横坐标满足x1>x2>1,根据图象可知y1<y2.(填“<”或“>”)
 已知二次函数y=-x2+2x+2,
已知二次函数y=-x2+2x+2,(1)用配方法把化为y=a(x+m)2+k的形式;
(2)选取适当的数据填入表,并在所给的直角坐标系内描点画出该抛物线的图象;
| x | … | … | |||||
| y | … | … |
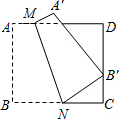 如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的点B′处,点A的对应点为点A′,且B′C=3,则B′N的长是( )
如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的点B′处,点A的对应点为点A′,且B′C=3,则B′N的长是( )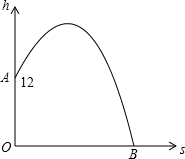 家在四楼的小明从窗口A向楼外掷出一个纸飞机,如果纸飞机下落过程值距离地面的高度h(米)与飞机的水平距离s(米)之间的关系式是h=-$\frac{1}{20}$s2+$\frac{2}{5}$s+m,其图象如图所示,那么这架纸飞机落地处点B与小明家所住的楼的相距20米.
家在四楼的小明从窗口A向楼外掷出一个纸飞机,如果纸飞机下落过程值距离地面的高度h(米)与飞机的水平距离s(米)之间的关系式是h=-$\frac{1}{20}$s2+$\frac{2}{5}$s+m,其图象如图所示,那么这架纸飞机落地处点B与小明家所住的楼的相距20米. 用8m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长,宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?
用8m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长,宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?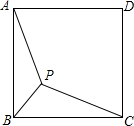 如图,已知点P是正方形ABCD内的一点,连结PA、PB、PC.若PA=4,PB=2,∠APB=135°,则PC的长为2$\sqrt{6}$.
如图,已知点P是正方形ABCD内的一点,连结PA、PB、PC.若PA=4,PB=2,∠APB=135°,则PC的长为2$\sqrt{6}$.