题目内容
2.在等腰△ABC和等腰△DEF中,∠A与∠D是顶角,下列判断不正确的是( )| A. | ∠A=∠D时,两三角形相似 | B. | ∠A=∠E时,两三角形相似 | ||
| C. | ∠B=∠E时,两三角形相似 | D. | $\frac{AB}{BC}=\frac{DF}{EF}$时,两三角形相似 |
分析 根据等腰三角形的性质和三角形内角和定理,由∠A=∠D时,则∠B=∠C=∠E=∠F,则根据有两组角对应相等的两个三角形相似可对A进行判断;由∠A=∠E得不到第二组角对应相等,则可对B进行判断;根据等腰三角形的性质,由∠B=∠E时,则∠B=∠C=∠E=∠F,则根据有两组角对应相等的两个三角形相似可对C进行判断;根据等腰三角形的性质和三组对应边的比相等的两个三角形相似可对D进行判断.
解答 解:A、∠A=∠D时,则∠B=∠C=∠E=∠F,所以△ABC∽△DEF,所以A选项的判断正确;
B、∠A=∠E时,不能判断△ABC∽△DEF,所以B选项的判断不正确;
C、∠B=∠E时,则∠B=∠C=∠E=∠F,所以△ABC∽△DEF,所以C选项的判断正确;
D、若$\frac{AB}{BC}$=$\frac{DF}{EF}$,则$\frac{AB}{DF}$=$\frac{BC}{EF}$,所以$\frac{AB}{DF}$=$\frac{AC}{DE}$=$\frac{BC}{EF}$,所以D选项的判断正确.
故选B.
点评 本题考查了相似三角形的判定:三组对应边的比相等的两个三角形相似;两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.也考查了等腰三角形的性质.

练习册系列答案
相关题目
12.将方程(x+1)(x-2)=2化为一元二次方程的一般形式,正确的是( )
| A. | x2-x-2=2 | B. | x2-x-4=0 | C. | x2-x=0 | D. | x2+x-4=0 |
13.下列各组数据分别是三角形三边长,是直角三角形的三边长的一组为( )
| A. | 5,6,7 | B. | 2,3,4 | C. | 8,15,17 | D. | 4,5,6 |
7.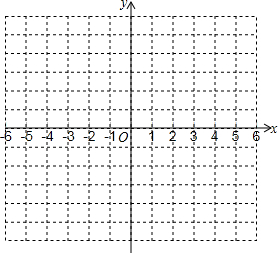 已知二次函数y=-x2+2x+2,
已知二次函数y=-x2+2x+2,
(1)用配方法把化为y=a(x+m)2+k的形式;
(2)选取适当的数据填入表,并在所给的直角坐标系内描点画出该抛物线的图象;
(3)若该抛物线上两点A(x1,y1),B(x2,y2)的横坐标满足x1>x2>1,根据图象可知y1<y2.(填“<”或“>”)
 已知二次函数y=-x2+2x+2,
已知二次函数y=-x2+2x+2,(1)用配方法把化为y=a(x+m)2+k的形式;
(2)选取适当的数据填入表,并在所给的直角坐标系内描点画出该抛物线的图象;
| x | … | … | |||||
| y | … | … |
 已知:△ABC的三个角度数的比∠A:∠B:∠C=1:2:3
已知:△ABC的三个角度数的比∠A:∠B:∠C=1:2:3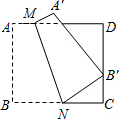 如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的点B′处,点A的对应点为点A′,且B′C=3,则B′N的长是( )
如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的点B′处,点A的对应点为点A′,且B′C=3,则B′N的长是( ) 用8m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长,宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?
用8m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长,宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少? 如图,⊙O与⊙O1交于A、B两点,O1点在⊙O上,AC是⊙O直径,AD是⊙O1直径,连结CD,求证:AC=CD.
如图,⊙O与⊙O1交于A、B两点,O1点在⊙O上,AC是⊙O直径,AD是⊙O1直径,连结CD,求证:AC=CD.