题目内容
6.已知:a,b,c是非零有理数,且a+b+c=0,求$\frac{a}{|a|}$+$\frac{b}{|b|}$+$\frac{c}{|c|}$的值.分析 根据a、b、c是非零实数,且a+b+c=0,可知a,b,c为两正一负或两负一正,按两种情况分别讨论代数式的可能的取值,再求所有可能的值即可.
解答 解:∵a、b、c是非零实数,且a+b+c=0,
∴a,b,c为两正一负或两负一正.
①当a,b,c为两正一负时:$\frac{a}{|a|}$+$\frac{b}{|b|}$+$\frac{c}{|c|}$=1+1-1=1;
②当a,b,c为两负一正时:$\frac{a}{|a|}$+$\frac{b}{|b|}$+$\frac{c}{|c|}$=-1-1+1=-1.
故$\frac{a}{|a|}$+$\frac{b}{|b|}$+$\frac{c}{|c|}$的所有可能的值为±1.
点评 本题考查了代数式求值,涉及到绝对值、非零实数的性质等知识点,注意分情况讨论未知数的取值,不要漏解.

练习册系列答案
相关题目
16.汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图1).图2是由弦图变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3.若S1+S2+S3=10,则S2的值是( )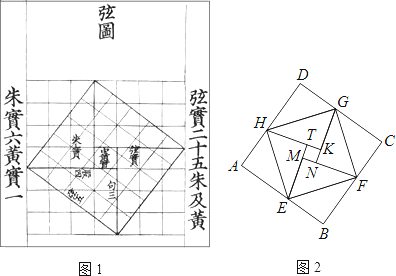

| A. | $\frac{11}{3}$ | B. | $\frac{10}{3}$ | C. | 3 | D. | $\frac{8}{3}$ |
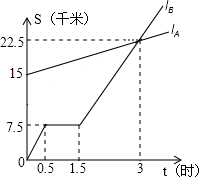 如图,yA和yB分别表示A步行和B骑自行车在同一路上行驶时路程s(千米)与时间t(时)的关系,已知两人同时出发,观察图象回答问题:
如图,yA和yB分别表示A步行和B骑自行车在同一路上行驶时路程s(千米)与时间t(时)的关系,已知两人同时出发,观察图象回答问题: 已知:△ABC的三个角度数的比∠A:∠B:∠C=1:2:3
已知:△ABC的三个角度数的比∠A:∠B:∠C=1:2:3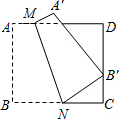 如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的点B′处,点A的对应点为点A′,且B′C=3,则B′N的长是( )
如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的点B′处,点A的对应点为点A′,且B′C=3,则B′N的长是( ) 用8m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长,宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?
用8m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长,宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少? 如图,△ABC经过旋转变换得到△AB′C′,若∠CAC′=35°,则∠BAB′=35度.
如图,△ABC经过旋转变换得到△AB′C′,若∠CAC′=35°,则∠BAB′=35度.