题目内容
11.如图,P是$\widehat{AB}$所对弦AB上一动点,过点P作PM⊥AB交$\widehat{AB}$于点M,连接MB,过点P作PN⊥MB于点N.已知AB=6cm,设A、P两点间的距离为x cm,P、N两点间的距离为y cm.(当点P与点A或点B重合时,y的值为0)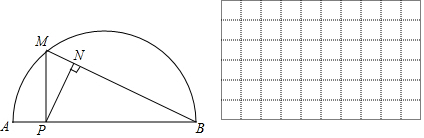
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
| x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y/cm | 0 | 2.0 | 2.3 | 2.1 | 1.6 | 0.9 | 0 |
(2)建立平面直角坐标系,描出已补全后的表中各对对应值为坐标的点,画出该函数的图象.
(3)结合画出的函数图象,解决问题:当△PAN为等腰三角形时,AP的长度约为2.2cm.
分析 (1)利用取点,测量的方法,即可解决问题;
(2)利用描点法,画出函数图象即可;
(3)作出直线y=x与图象的交点,交点的横坐标即可AP的长.
解答 解:(1)通过取点、画图、测量可得x=4时,y=1.6cm,
故答案为1.6.
(2)利用描点法,图象如图所示.
(3)当△PAN为等腰三角形时,x=y,作出直线y=x与图象的交点坐标为(2.2,2.2),
∴△PAN为等腰三角形时,PA=2.2cm.
故答案为2.2.
点评 本题考查圆综合题、坐标与图形的关系等知识,解题的关键是理解题意,学会用测量法、图象法解决实际问题,属于中考压轴题.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于$\frac{1}{2}BF$长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于$\frac{1}{2}BF$长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF. 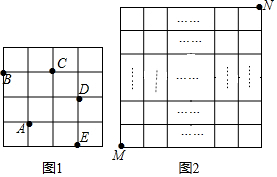
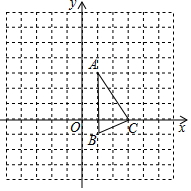 如图,△ABC位于直角坐标系内,且三个顶点均在正方形的网格的顶点上.
如图,△ABC位于直角坐标系内,且三个顶点均在正方形的网格的顶点上.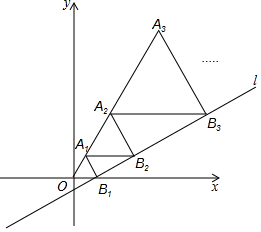 如图,在平面直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是$\frac{{2}^{2017}-1}{2}$.
如图,在平面直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是$\frac{{2}^{2017}-1}{2}$.