题目内容
20.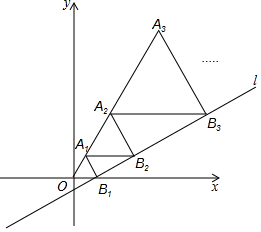 如图,在平面直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是$\frac{{2}^{2017}-1}{2}$.
如图,在平面直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是$\frac{{2}^{2017}-1}{2}$.
分析 先根据直线l:y=$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$与x轴交于点B1,可得B1(1,0),OB1=1,∠OB1D=30°,再,过A1作A1A⊥OB1于A,过A2作A2B⊥A1B2于B,过A3作A3C⊥A2B3于C,根据等边三角形的性质以及含30°角的直角三角形的性质,分别求得A1的横坐标为$\frac{{2}^{1}-1}{2}$,A2的横坐标为$\frac{{2}^{2}-1}{2}$,A3的横坐标为$\frac{{2}^{3}-1}{2}$,进而得到An的横坐标为$\frac{{2}^{n}-1}{2}$,据此可得点A2017的横坐标.
解答  解:由直线l:y=$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$与x轴交于点B1,可得B1(1,0),D(-$\frac{\sqrt{3}}{3}$,0),
解:由直线l:y=$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$与x轴交于点B1,可得B1(1,0),D(-$\frac{\sqrt{3}}{3}$,0),
∴OB1=1,∠OB1D=30°,
如图所示,过A1作A1A⊥OB1于A,则OA=$\frac{1}{2}$OB1=$\frac{1}{2}$,
即A1的横坐标为$\frac{1}{2}$=$\frac{{2}^{1}-1}{2}$,
由题可得∠A1B2B1=∠OB1D=30°,∠B2A1B1=∠A1B1O=60°,
∴∠A1B1B2=90°,
∴A1B2=2A1B1=2,
过A2作A2B⊥A1B2于B,则A1B=$\frac{1}{2}$A1B2=1,
即A2的横坐标为$\frac{1}{2}$+1=$\frac{3}{2}$=$\frac{{2}^{2}-1}{2}$,
过A3作A3C⊥A2B3于C,
同理可得,A2B3=2A2B2=4,A2C=$\frac{1}{2}$A2B3=2,
即A3的横坐标为$\frac{1}{2}$+1+2=$\frac{7}{2}$=$\frac{{2}^{3}-1}{2}$,
同理可得,A4的横坐标为$\frac{1}{2}$+1+2+4=$\frac{15}{2}$=$\frac{{2}^{4}-1}{2}$,
由此可得,An的横坐标为$\frac{{2}^{n}-1}{2}$,
∴点A2017的横坐标是$\frac{{2}^{2017}-1}{2}$,
故答案为:$\frac{{2}^{2017}-1}{2}$.
点评 本题主要考查了一次函数图象上点的坐标特征以及等边三角形的性质的运用,解决问题的关键是依据等边三角形的性质找出规律,求得An的横坐标为$\frac{{2}^{n}-1}{2}$.

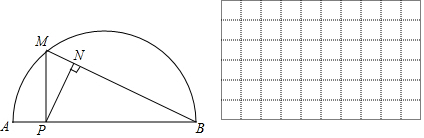
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
| x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y/cm | 0 | 2.0 | 2.3 | 2.1 | 1.6 | 0.9 | 0 |
(2)建立平面直角坐标系,描出已补全后的表中各对对应值为坐标的点,画出该函数的图象.
(3)结合画出的函数图象,解决问题:当△PAN为等腰三角形时,AP的长度约为2.2cm.
| A. | 当AB=BC时,它是菱形 | B. | 当AC=BD时,它是正方形 | ||
| C. | 当∠ABC=90°时,它是矩形 | D. | 当AC⊥BD时,它是菱形 |
 如图,菱形ABCD的对角线相交于点O,对角线AC=6,BD=8,点E在BC的延长线上,且OE=OB,连接DE.
如图,菱形ABCD的对角线相交于点O,对角线AC=6,BD=8,点E在BC的延长线上,且OE=OB,连接DE.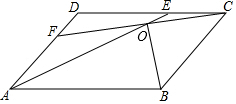 如图,在平行四边形ABCD中,AE=CF,AE与CF交于点O.求证:∠AOB=∠COB.
如图,在平行四边形ABCD中,AE=CF,AE与CF交于点O.求证:∠AOB=∠COB.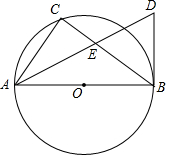 如图,AB是⊙O直径,点C在⊙O上,AD平分∠CAB,BD是⊙O的切线,AD与BC相交于点E.
如图,AB是⊙O直径,点C在⊙O上,AD平分∠CAB,BD是⊙O的切线,AD与BC相交于点E. 如图,四边形ABCD内接于⊙O,点E在BC的延长线上,若∠BOD=120°,则∠DCE=60°.
如图,四边形ABCD内接于⊙O,点E在BC的延长线上,若∠BOD=120°,则∠DCE=60°.