题目内容
2.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.从一个格点移动到与之相距$\sqrt{5}$的另一个格点的运动称为一次跳马变换.例如,在4×4的正方形网格图形中(如图1),从点A经过一次跳马变换可以到达点B,C,D,E等处.现有20×20的正方形网格图形(如图2),则从该正方形的顶点M经过跳马变换到达与其相对的顶点N,最少需要跳马变换的次数是( )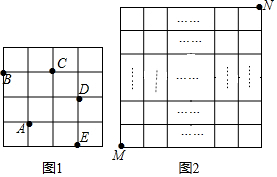
| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
分析 根据从一个格点移动到与之相距$\sqrt{5}$的另一个格点的运动称为一次跳马变换,计算出按A-C-F的方向连续变换10次后点M的位置,再根据点N的位置进行适当的变换,即可得到变换总次数.
解答 解:如图1,连接AC,CF,则AF=3$\sqrt{2}$,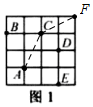
∴两次变换相当于向右移动3格,向上移动3格,
又∵MN=20$\sqrt{2}$,
∴20$\sqrt{2}$÷3$\sqrt{2}$=$\frac{20}{3}$,(不是整数)
∴按A-C-F的方向连续变换10次后,相当于向右移动了10÷2×3=15格,向上移动了10÷2×3=15格,
此时M位于如图所示的5×5的正方形网格的点G处,再按如图所示的方式变换4次即可到达点N处,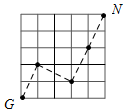
∴从该正方形的顶点M经过跳马变换到达与其相对的顶点N,最少需要跳马变换的次数是14次,
故选:B.
点评 本题主要考查了几何变换的类型以及勾股定理的运用,解题时注意:在平移变换下,对应线段平行且相等,两对应点连线段与给定的有向线段平行(共线)且相等.解决问题的关键是找出变换的规律.

练习册系列答案
相关题目
11.如图,P是$\widehat{AB}$所对弦AB上一动点,过点P作PM⊥AB交$\widehat{AB}$于点M,连接MB,过点P作PN⊥MB于点N.已知AB=6cm,设A、P两点间的距离为x cm,P、N两点间的距离为y cm.(当点P与点A或点B重合时,y的值为0)
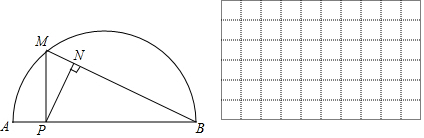
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出已补全后的表中各对对应值为坐标的点,画出该函数的图象.
(3)结合画出的函数图象,解决问题:当△PAN为等腰三角形时,AP的长度约为2.2cm.

小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
| x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y/cm | 0 | 2.0 | 2.3 | 2.1 | 1.6 | 0.9 | 0 |
(2)建立平面直角坐标系,描出已补全后的表中各对对应值为坐标的点,画出该函数的图象.
(3)结合画出的函数图象,解决问题:当△PAN为等腰三角形时,AP的长度约为2.2cm.
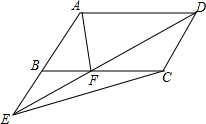 如图,E是?ABCD中AB延长线上一点,ED交BC于点F,求证:S△ABF=S△CEF.
如图,E是?ABCD中AB延长线上一点,ED交BC于点F,求证:S△ABF=S△CEF.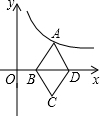 如图,已知菱形ABCD的对角线BD在x轴上,A点在y=$\frac{k}{x}$(x>0)的图象上,C点的坐标为(2,-1),则k=2.
如图,已知菱形ABCD的对角线BD在x轴上,A点在y=$\frac{k}{x}$(x>0)的图象上,C点的坐标为(2,-1),则k=2. 如图,菱形ABCD的对角线相交于点O,对角线AC=6,BD=8,点E在BC的延长线上,且OE=OB,连接DE.
如图,菱形ABCD的对角线相交于点O,对角线AC=6,BD=8,点E在BC的延长线上,且OE=OB,连接DE.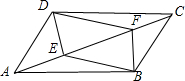 已知:如图,四边形DEBF是平行四边形,且AE=CF.
已知:如图,四边形DEBF是平行四边形,且AE=CF.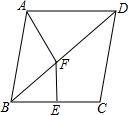 如图,在菱形ABCD中,∠ABC=40°,BC的垂直平分线EF交对角线BD于点F.连接AF,则∠DAF的度数为120°.
如图,在菱形ABCD中,∠ABC=40°,BC的垂直平分线EF交对角线BD于点F.连接AF,则∠DAF的度数为120°.