题目内容
1. 如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于$\frac{1}{2}BF$长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于$\frac{1}{2}BF$长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF. (1)四边形ABEF是B
A.矩形 B.菱形 C.正方形 D.无法确定
(2)若四边形ABEF的周长为40,AE,BF相交于点O,且BF=10,试求
①∠ABC的度数;
②AE的长.
分析 (1)先根据四边形ABCD是平行四边形得出AD∥BC,再由AB=AF即可得出结论;
(2)①先根据菱形的周长求出其边长,再由BF=10得出△ABF是等边三角形,据此可得出结论;
②先根据勾股定理求出AO的长,再由菱形的性质即可得出结论.
解答 解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC.
∵AB=AF,
∴四边形ABEF是菱形.
故答案为:B;
(2)①∵四边形ABEF是菱形,且周长为40,
∴AB=AF=40÷4=10.
∵BF=10,
∴△ABF是等边三角形,
∴∠ABF=60°,
∴∠ABC=2∠ABF=120°;
②∵AF=10,
∴OF=5.
∵AE垂直平分BF,
∴AO=$\sqrt{A{F}^{2}-F{O}^{2}}$=5$\sqrt{3}$,
∴AE=2AO=10$\sqrt{3}$.
点评 本题考查的是作图-基本作图,熟知角平分线的作法及菱形的性质是解答此题的关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
16.多项式m2-m与多项式2m2-4m+2的公因式是( )
| A. | m-1 | B. | m+1 | C. | m2-1 | D. | (m-1)2 |
11.如图,P是$\widehat{AB}$所对弦AB上一动点,过点P作PM⊥AB交$\widehat{AB}$于点M,连接MB,过点P作PN⊥MB于点N.已知AB=6cm,设A、P两点间的距离为x cm,P、N两点间的距离为y cm.(当点P与点A或点B重合时,y的值为0)
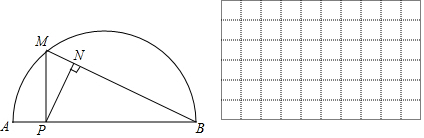
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出已补全后的表中各对对应值为坐标的点,画出该函数的图象.
(3)结合画出的函数图象,解决问题:当△PAN为等腰三角形时,AP的长度约为2.2cm.

小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
| x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y/cm | 0 | 2.0 | 2.3 | 2.1 | 1.6 | 0.9 | 0 |
(2)建立平面直角坐标系,描出已补全后的表中各对对应值为坐标的点,画出该函数的图象.
(3)结合画出的函数图象,解决问题:当△PAN为等腰三角形时,AP的长度约为2.2cm.
 如图,E是?ABCD中AB延长线上一点,ED交BC于点F,求证:S△ABF=S△CEF.
如图,E是?ABCD中AB延长线上一点,ED交BC于点F,求证:S△ABF=S△CEF.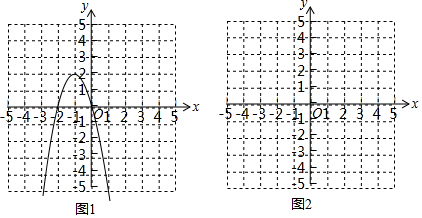
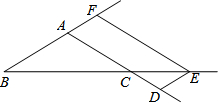 在△ABC中,AD=BF,点D,E,F分别是AC,BC,BA延长线上的点,四边形ADEF为平行四边形.
在△ABC中,AD=BF,点D,E,F分别是AC,BC,BA延长线上的点,四边形ADEF为平行四边形.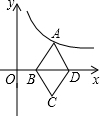 如图,已知菱形ABCD的对角线BD在x轴上,A点在y=$\frac{k}{x}$(x>0)的图象上,C点的坐标为(2,-1),则k=2.
如图,已知菱形ABCD的对角线BD在x轴上,A点在y=$\frac{k}{x}$(x>0)的图象上,C点的坐标为(2,-1),则k=2. 如图,菱形ABCD的对角线相交于点O,对角线AC=6,BD=8,点E在BC的延长线上,且OE=OB,连接DE.
如图,菱形ABCD的对角线相交于点O,对角线AC=6,BD=8,点E在BC的延长线上,且OE=OB,连接DE.