题目内容
19.已知二次函数y=x2-(3m-1)x+2m2-2m,其中m>-1.(1)若二次函数关于x轴对称,则m的值为$\frac{1}{3}$;
(2)二次函数与x轴交于A(x1,0),B(x2,0)(x1<x2)两点,且-1≤$\frac{1}{2}$x1-$\frac{1}{3}$x2≤1,试求m的取值范围;
(3)当1≤x≤3时,二次函数的最小值是-1,求m的值.
分析 (1)根据二次函数关于x轴对称,则b=0即可解题;
(2)根据二次函数求根公式可以求得x1和x2的值(用m表示),即可解题;
(3)分类讨论,①对称轴在x=1左侧,②对称轴在x=3右侧,③对称轴在x=1和x=3中间,即可求得m的值,即可解题.
解答 解:(1)二次函数关于x轴对称,则3m-1=0,解得:m=$\frac{1}{3}$;
故答案为 $\frac{1}{3}$;
(2)y=x2-(3m-1)x+2m2-2m=0时,
△=(3m-1)2-4(2m2-2m)=(m-1)2,
∴x1=$\frac{(3m-1)-\sqrt{{(m+1)}^{2}}}{2}$=m-1,x2=$\frac{(3m-1)+\sqrt{{(m+1)}^{2}}}{2}$=2m,
∵-1≤$\frac{1}{2}$x1-$\frac{1}{3}$x2≤1,
∴-1≤$\frac{m-1}{2}$-$\frac{2m}{3}$≤1,
整理得:-9≤m≤3,
∵m>-1,
∴-1<m≤3;
(3)①当对称轴x=$\frac{3m-1}{2}$≤1时,x=1,二次函数有最小值,此时-1<m≤1,
代入x=1得:1-(3m-1)+2m2-2m=-1,
化简得:2m2-5m+3=0,
解得:m=1,或m=$\frac{3}{2}$(舍去);
②当对称轴x=$\frac{3m-1}{2}$≥3时,x=3,二次函数有最小值,此时m≥$\frac{7}{3}$,
代入x=3得:9-3(3m-1)+2m2-2m=-1,
化简得:2m2-11m+13=0,
解得:m=$\frac{11+\sqrt{17}}{4}$,或m=$\frac{11-\sqrt{17}}{4}$(舍去);
③当对称轴1<x=$\frac{3m-1}{2}$<3时,x=$\frac{3m-1}{2}$时,二次函数有最小值,此时1<m<$\frac{7}{3}$,
代入x=$\frac{3m-1}{2}$得:$\frac{{(3m-1)}^{2}}{4}$-$\frac{{(3m-1)}^{2}}{2}$+2m2-2m=-1,
化简得:m2+2m-3=0,
解得:m=1或m=-3,(均舍去)
综上所述,m的值为:$\frac{11+\sqrt{17}}{4}$或1.
点评 本题考查了二次函数的求根公式,考查了二次函数的最小值问题,本题中运用分类讨论思想是解题的关键.

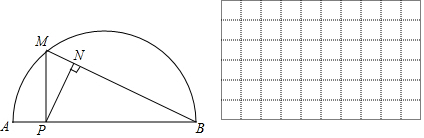
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东的探究过程,请补充完整:
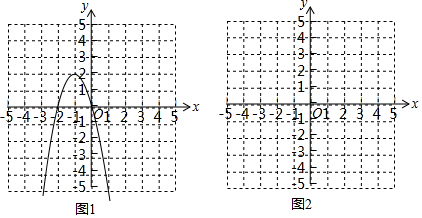
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
| x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y/cm | 0 | 2.0 | 2.3 | 2.1 | 1.6 | 0.9 | 0 |
(2)建立平面直角坐标系,描出已补全后的表中各对对应值为坐标的点,画出该函数的图象.
(3)结合画出的函数图象,解决问题:当△PAN为等腰三角形时,AP的长度约为2.2cm.
 如图,菱形ABCD的对角线相交于点O,对角线AC=6,BD=8,点E在BC的延长线上,且OE=OB,连接DE.
如图,菱形ABCD的对角线相交于点O,对角线AC=6,BD=8,点E在BC的延长线上,且OE=OB,连接DE.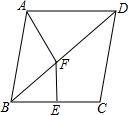 如图,在菱形ABCD中,∠ABC=40°,BC的垂直平分线EF交对角线BD于点F.连接AF,则∠DAF的度数为120°.
如图,在菱形ABCD中,∠ABC=40°,BC的垂直平分线EF交对角线BD于点F.连接AF,则∠DAF的度数为120°.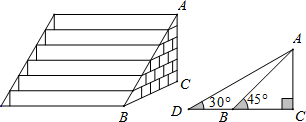
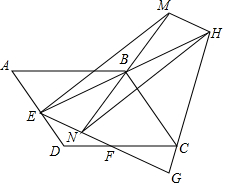 如图,平行四边形ABCD中,AD=4,∠A=60°,E,F分别是AD,CD边上的中点,且EF=$\sqrt{19}$,连接EB并延长至H,使BE=BH,连接HC并延长与EF延长线交于G,N是线段EG上一动点,以EH为对角线的所有平行四边形ENHM中,MN的最小值是$\frac{18\sqrt{57}}{19}$.
如图,平行四边形ABCD中,AD=4,∠A=60°,E,F分别是AD,CD边上的中点,且EF=$\sqrt{19}$,连接EB并延长至H,使BE=BH,连接HC并延长与EF延长线交于G,N是线段EG上一动点,以EH为对角线的所有平行四边形ENHM中,MN的最小值是$\frac{18\sqrt{57}}{19}$.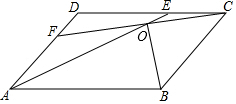 如图,在平行四边形ABCD中,AE=CF,AE与CF交于点O.求证:∠AOB=∠COB.
如图,在平行四边形ABCD中,AE=CF,AE与CF交于点O.求证:∠AOB=∠COB. 如图,四边形ABCD内接于⊙O,点E在BC的延长线上,若∠BOD=120°,则∠DCE=60°.
如图,四边形ABCD内接于⊙O,点E在BC的延长线上,若∠BOD=120°,则∠DCE=60°.