题目内容
16.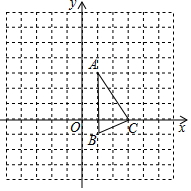 如图,△ABC位于直角坐标系内,且三个顶点均在正方形的网格的顶点上.
如图,△ABC位于直角坐标系内,且三个顶点均在正方形的网格的顶点上.(1)将△ABC平移后得到△A1B1C1,点A(1,3)对应点A1坐标是(-2,1),B,C对应点分别为B1,C1,画出△A1B1C1,并写出点B1,C1的坐标.
(2)将△A1B1C1顶点A1,B1,C1的横、纵坐标分别乘以-2,依次作为点A2,B2,C2的横、纵坐标,画出△A2,B2,C2.
分析 (1)根据点A(1,3)对应点A1坐标是(-2,1),可知平移的方向与距离为向左平移3个单位,再向下平移2个单位,进而得到B1,C1的位置;
(2)根据△A1B1C1顶点A1,B1,C1的横、纵坐标分别乘以-2,依次作为点A2,B2,C2的横、纵坐标,可知A2,B2,C2的坐标分别为(4,-2),(4,6),(0,4),据此可画出△A2B2C2.
解答 解:(1)如图所示,△A1B1C1即为所求,由题可得,B1(-2,-3),C1(0,-2);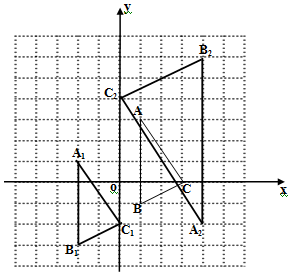
(2)如图所示,△A2B2C2即为所求.
点评 本题主要考查了利用平移变换进行作图,作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.如图,P是$\widehat{AB}$所对弦AB上一动点,过点P作PM⊥AB交$\widehat{AB}$于点M,连接MB,过点P作PN⊥MB于点N.已知AB=6cm,设A、P两点间的距离为x cm,P、N两点间的距离为y cm.(当点P与点A或点B重合时,y的值为0)
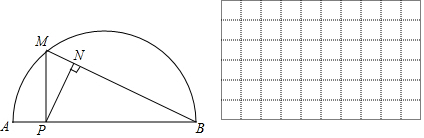
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出已补全后的表中各对对应值为坐标的点,画出该函数的图象.
(3)结合画出的函数图象,解决问题:当△PAN为等腰三角形时,AP的长度约为2.2cm.

小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
| x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y/cm | 0 | 2.0 | 2.3 | 2.1 | 1.6 | 0.9 | 0 |
(2)建立平面直角坐标系,描出已补全后的表中各对对应值为坐标的点,画出该函数的图象.
(3)结合画出的函数图象,解决问题:当△PAN为等腰三角形时,AP的长度约为2.2cm.
1.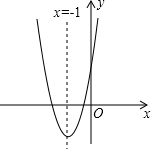 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,给出下列结论:
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,给出下列结论:
①b2=4ac;②abc>0;③a>c;④4a-2b+c>0,其中正确的个数有( )
 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,给出下列结论:
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,给出下列结论:①b2=4ac;②abc>0;③a>c;④4a-2b+c>0,其中正确的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
| A. | 当AB=BC时,它是菱形 | B. | 当AC=BD时,它是正方形 | ||
| C. | 当∠ABC=90°时,它是矩形 | D. | 当AC⊥BD时,它是菱形 |
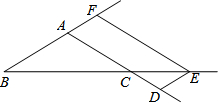 在△ABC中,AD=BF,点D,E,F分别是AC,BC,BA延长线上的点,四边形ADEF为平行四边形.
在△ABC中,AD=BF,点D,E,F分别是AC,BC,BA延长线上的点,四边形ADEF为平行四边形.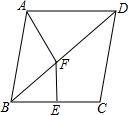 如图,在菱形ABCD中,∠ABC=40°,BC的垂直平分线EF交对角线BD于点F.连接AF,则∠DAF的度数为120°.
如图,在菱形ABCD中,∠ABC=40°,BC的垂直平分线EF交对角线BD于点F.连接AF,则∠DAF的度数为120°.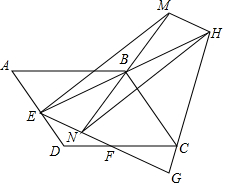 如图,平行四边形ABCD中,AD=4,∠A=60°,E,F分别是AD,CD边上的中点,且EF=$\sqrt{19}$,连接EB并延长至H,使BE=BH,连接HC并延长与EF延长线交于G,N是线段EG上一动点,以EH为对角线的所有平行四边形ENHM中,MN的最小值是$\frac{18\sqrt{57}}{19}$.
如图,平行四边形ABCD中,AD=4,∠A=60°,E,F分别是AD,CD边上的中点,且EF=$\sqrt{19}$,连接EB并延长至H,使BE=BH,连接HC并延长与EF延长线交于G,N是线段EG上一动点,以EH为对角线的所有平行四边形ENHM中,MN的最小值是$\frac{18\sqrt{57}}{19}$.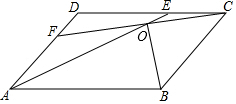 如图,在平行四边形ABCD中,AE=CF,AE与CF交于点O.求证:∠AOB=∠COB.
如图,在平行四边形ABCD中,AE=CF,AE与CF交于点O.求证:∠AOB=∠COB.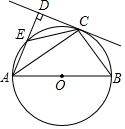 如图,AB为⊙O的直径,C为⊙O上一点,AD与过点C的切线互相垂直,垂足为点D,AD交⊙O于点E,连接CE,CB.
如图,AB为⊙O的直径,C为⊙O上一点,AD与过点C的切线互相垂直,垂足为点D,AD交⊙O于点E,连接CE,CB.