题目内容
13.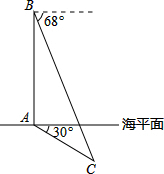 俄罗斯和中国2015年将在地中海海域和太平洋地区举行联合演习,我军自主演习时军舰A测得潜艇C的俯角为30°,位于军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5,$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
俄罗斯和中国2015年将在地中海海域和太平洋地区举行联合演习,我军自主演习时军舰A测得潜艇C的俯角为30°,位于军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5,$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
分析 过点C作CD⊥BA的延长线于点D,则AD即为潜艇C的下潜深度,设AD=x,则BD=BA+AD=1000+x,再由锐角三角函数的定义得出CD及BD的长,进而可得出结论.
解答 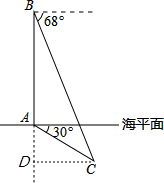 解:过点C作CD⊥BA的延长线于点D,则AD即为潜艇C的下潜深度,
解:过点C作CD⊥BA的延长线于点D,则AD即为潜艇C的下潜深度,
根据题意得,∠ACD=30°,∠BCD=68°,
设AD=x,则BD=BA+AD=1000+x.
在Rt△ACD中,CD=$\frac{AD}{tan∠ACD}$=$\sqrt{3}$x.
在Rt△BCD中,BD=CD•tan68°,
∴1000+x=$\sqrt{3}$x•tan68°,解得x=$\frac{1000}{\sqrt{3}•tan68°-1}$≈$\frac{1000}{1.7×2.5-1}$≈308(米).
∴潜艇的下潜深度为308米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
1.如表,从左到右在每个小格子中填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
(1)可求得c=9,第2015个格子中的数为-5;
(2)如果x、y为前三个格子中的任意两个数,那么所有的|x-y|的和可以通过计算|9-a|+|a-9|+|9-b|+|b-9|+|a-b|+|b-a|得到,求所有的|x-y|的和;
(3)前m个格子中所填整数之和是否可能为2015?若能,求m的值;若不能,请说出理由.
| 9 | a | b | c | -5 | 1 | … |
(2)如果x、y为前三个格子中的任意两个数,那么所有的|x-y|的和可以通过计算|9-a|+|a-9|+|9-b|+|b-9|+|a-b|+|b-a|得到,求所有的|x-y|的和;
(3)前m个格子中所填整数之和是否可能为2015?若能,求m的值;若不能,请说出理由.
5.某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核,三人各项得分如表:
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按50%,30%,20%的比例计入总分.根据规定,请你说明谁将被录用.
| 笔试 | 面试 | 体能 | |
| 甲 | 84 | 78 | 90 |
| 乙 | 85 | 80 | 75 |
| 丙 | 80 | 90 | 73 |
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按50%,30%,20%的比例计入总分.根据规定,请你说明谁将被录用.
 在平面直角坐标系中,A(5,4)、B(4,2)、C(1,0).
在平面直角坐标系中,A(5,4)、B(4,2)、C(1,0).
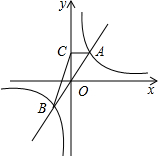 如图,正比例函数y1=mx(m>0)的图象与反比例函数y2=$\frac{k}{x}$(k≠0)的图象交于点A(n,4)和点B,AC⊥y轴,垂足为M,△ACB的面积为8.
如图,正比例函数y1=mx(m>0)的图象与反比例函数y2=$\frac{k}{x}$(k≠0)的图象交于点A(n,4)和点B,AC⊥y轴,垂足为M,△ACB的面积为8.