题目内容
3.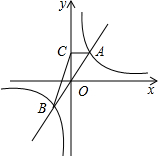 如图,正比例函数y1=mx(m>0)的图象与反比例函数y2=$\frac{k}{x}$(k≠0)的图象交于点A(n,4)和点B,AC⊥y轴,垂足为M,△ACB的面积为8.
如图,正比例函数y1=mx(m>0)的图象与反比例函数y2=$\frac{k}{x}$(k≠0)的图象交于点A(n,4)和点B,AC⊥y轴,垂足为M,△ACB的面积为8.(1)求点A和点B的坐标;
(2)求正比例函数与反比例函数的解析式;
(3)当y1>y2时,求实数x的取值范围.
分析 (1)首先根据反比例函数与正比例函数的图象特征,可知A、B两点关于原点对称,则O为线段AB的中点,故△BOC的面积等于△AOC的面积,都等于2,然后由反比例函数的比例系数k的几何意义,可知△AOC的面积等于 $\frac{1}{2}$|k|,从而求出k的值,即得到这个反比例函数的解析式,于是得到结论;
(2)正比例函数和反比例函数图象上点的坐标特征即可得到结论;
(3)由图象即可得到结论.
解答 解:∵反比例函数与正比例函数的图象相交于A、B两点,
∴A、B两点关于原点对称,
∴OA=OB,
∴△BOC的面积=△AOC的面积=8÷2=4,
又∵A是反比例函数y2=$\frac{k}{x}$图象上的点,且AC⊥y轴于点C,
∴△AOC的面积=$\frac{1}{2}$|k|,
∴$\frac{1}{2}$|k|=4,
∵k>0,
∴k=8,
故这个反比例函数的解析式为 y=$\frac{8}{x}$,
∵A(n,4),
∴A(2,4),
∵A、B两点关于原点对称,
∴B(-2,-4);
(2)∵正比例函数y1=mx(m>0)的图象与反比例函数y2=$\frac{k}{x}$(k≠0)的图象交于点A(2,4),
∴m=2,
∴正比例函数的解析式是y=2x,反比例函数的解析式为y=$\frac{8}{x}$;
(3)由图象知当y1>y2时,x的取值范围是-2<x<0或x>2.
点评 本题主要考查了三角形一边上的中线将三角形的面积二等分及反比例函数的比例系数k的几何意义:反比例函数图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系,即S=$\frac{1}{2}$|k|.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
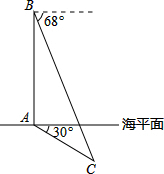 俄罗斯和中国2015年将在地中海海域和太平洋地区举行联合演习,我军自主演习时军舰A测得潜艇C的俯角为30°,位于军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5,$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
俄罗斯和中国2015年将在地中海海域和太平洋地区举行联合演习,我军自主演习时军舰A测得潜艇C的俯角为30°,位于军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5,$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)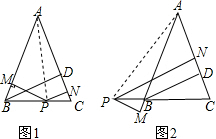 如图1,在△ABC中,AB=AC,BD是△ABC的高,P是BC边上一点,PN分别与直线AB,AC垂直,垂足分别为点M,N,求证:BD=PM+PN.
如图1,在△ABC中,AB=AC,BD是△ABC的高,P是BC边上一点,PN分别与直线AB,AC垂直,垂足分别为点M,N,求证:BD=PM+PN. 如图,在热气球上A处测得一栋大楼顶部B的俯角为23°,测得这栋大楼底部C的俯角为45°.已知热气球A处距地面的高度为180m,求这栋大楼的高度(精确到1m).(参考数据:sin23°=0.39,cos23°=0.92,tan23°=0.42)
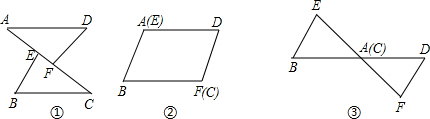
如图,在热气球上A处测得一栋大楼顶部B的俯角为23°,测得这栋大楼底部C的俯角为45°.已知热气球A处距地面的高度为180m,求这栋大楼的高度(精确到1m).(参考数据:sin23°=0.39,cos23°=0.92,tan23°=0.42) 如图,已知AE=CF,AD=BC,DF=BE.
如图,已知AE=CF,AD=BC,DF=BE.