题目内容
1.如表,从左到右在每个小格子中填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.| 9 | a | b | c | -5 | 1 | … |
(2)如果x、y为前三个格子中的任意两个数,那么所有的|x-y|的和可以通过计算|9-a|+|a-9|+|9-b|+|b-9|+|a-b|+|b-a|得到,求所有的|x-y|的和;
(3)前m个格子中所填整数之和是否可能为2015?若能,求m的值;若不能,请说出理由.
分析 (1)根据其中任意三个相邻格子中所填整数之和都相等,得出每三个数字一个循环,依次读下去,得c=9,a=-5,b=1,2015÷3=671余2,故2015个数为-5.
(2)通过分类讨论求出所有a、b的可能情况,求出结果即可,当取前19个格子中数字,这三个数,9出现了7次,-6和2各出现了6次,通过分类讨论求出所有s、t的可能情况,求出结果即可;
(3)计算三个格子和为5,而2015能被5整除,因此,n个格子中所填整数之和可以为2015.
解答 解:(1)∵任意三个相邻格子中所填整数之和都相等,
∴9+a+b=a+b+c,
解得c=9,
则a=-5,b=1,
所以,数据从左到右依次为9、-5、1、9、-5、1、…,
∵2015÷3=671…2,
∴第2015个格子中的整数与第2个格子中的数相同,为-5.
(2)|9-a|+|a-9|+|9-b|+|b-9|+|a-b|+|b-a|
=14+14+8+8+6+6
=56;
(3)能为2015.
理由:∵9-5+1=5,
2015÷5=403,
∴m=403×3=1209.
故答案为:9,-5.
点评 题目考查了数字的变化规律,通过表格中数字的变化,体会数字变化为学生们带来的快乐.题目整体较难,特别是(3)中的总结性求和,更能体现学生的解决问题能力.

练习册系列答案
相关题目
 为了美化环境,学校准备在如图所示的矩形ABCD空地上迸行绿化,规划在中间的一块四边形MNQP上种花,其余的四块三角形上铺设草坪,要求AM=AN=CP=CQ.已知BC=24米,AB=40米,设AN=x米,种花的面积为y1平方米,草坪面积y2平方米.
为了美化环境,学校准备在如图所示的矩形ABCD空地上迸行绿化,规划在中间的一块四边形MNQP上种花,其余的四块三角形上铺设草坪,要求AM=AN=CP=CQ.已知BC=24米,AB=40米,设AN=x米,种花的面积为y1平方米,草坪面积y2平方米.
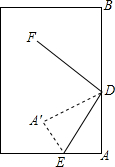 如图,斜折一页书的一角,使点A落在同一页书内的点A'处,DE为折痕,作DF平分∠A'DB,试猜想∠FDE的度数,并说明理由.
如图,斜折一页书的一角,使点A落在同一页书内的点A'处,DE为折痕,作DF平分∠A'DB,试猜想∠FDE的度数,并说明理由.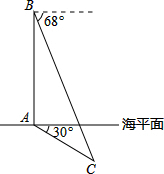 俄罗斯和中国2015年将在地中海海域和太平洋地区举行联合演习,我军自主演习时军舰A测得潜艇C的俯角为30°,位于军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5,$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
俄罗斯和中国2015年将在地中海海域和太平洋地区举行联合演习,我军自主演习时军舰A测得潜艇C的俯角为30°,位于军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5,$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)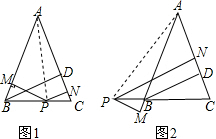 如图1,在△ABC中,AB=AC,BD是△ABC的高,P是BC边上一点,PN分别与直线AB,AC垂直,垂足分别为点M,N,求证:BD=PM+PN.
如图1,在△ABC中,AB=AC,BD是△ABC的高,P是BC边上一点,PN分别与直线AB,AC垂直,垂足分别为点M,N,求证:BD=PM+PN.