题目内容
2.宝塔中学自从开展“高校课堂”模式以来,在课堂上进行当堂测试效果很好.每节课40分钟教学,假设老师用于精讲的时间x(单位:分钟)与学生学习收益量y的关系如图示1所示,学生用于当堂检测的时间x(单位:分钟)与学习收益y的关系如图2所示(其中OA是抛物线的一部分,A为抛物线的顶点),且用于当堂检测的时间不超过用于精讲的时间.(1)求老师精讲的学生学习收益量y与用于精讲的时间x之间的函数关系式;
(2)求学生当堂检测的学习收益量y与用于当堂检测的时间x的函数关系式;
(3)问此“高效课堂”模式如何分配精讲和当堂检测的时间,才能使这学生在40分钟的学习收益总量最大?
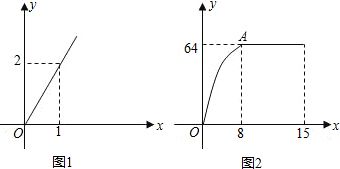
分析 (1)由图设该函数解析式为y=kx,即可依题意求出y与x的函数关系式.
(2)本题涉及分段函数的知识.需要注意的是x的取值范围依照分段函数的解法解出即可.
(3)设学生当堂检测的时间为x分钟(0≤x≤15),学生的学习收益总量为W,则老师在课堂用于精讲的时间为(40-x)分钟.用配方法的知识解答该题即可.
解答 解:(1)设y=kx,
把(1,2)代入,得:k=2,
∴y=2x,(0≤x≤40);
(2)当0≤x≤8时,设y=a(x-8)2+64,
把(0,0)代入,得:64a+64=0,
解得:a=-1,
∴y=-(x-8)2+64=-x2+16x,
当8<x≤15时,y=64;
(3)设学生当堂检测的时间为x分钟(0≤x≤15),学生的学习收益总量为W,则老师在课堂用于精讲的时间为(40-x)分钟,
当0≤x≤8时,W=-x2+16x+2(40-x)=-x2+14x+80=-(x-7)2+129,
当x=7时,Wmax=129;
当8≤x≤15时,W=64+2(40-x)=-2x+144,
∵W随x的增大而减小,
∴当x=8时,Wmax=128,
综上,当x=7时,W取得最大值129,此时40-x=33,
答:此“高效课堂”模式如何分配33分钟时间用于精讲、分配7分钟时间当堂检测,才能使这学生在40分钟的学习收益总量最大.
点评 本题考查了待定系数法求一次函数的解析式的运用,二次函数的运用,顶点式求二次函数的最大值的运用,解答时求出二次函数的解析式是关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
7.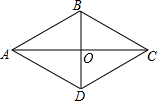 如图,已知某广场菱形花坛ABCD的周长是12米,∠BAD=60°,则花坛对角线AC的长等于( )
如图,已知某广场菱形花坛ABCD的周长是12米,∠BAD=60°,则花坛对角线AC的长等于( )
 如图,已知某广场菱形花坛ABCD的周长是12米,∠BAD=60°,则花坛对角线AC的长等于( )
如图,已知某广场菱形花坛ABCD的周长是12米,∠BAD=60°,则花坛对角线AC的长等于( )| A. | 3$\sqrt{3}$米 | B. | 4米 | C. | 2$\sqrt{3}$米 | D. | 2米 |
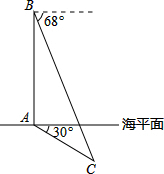 俄罗斯和中国2015年将在地中海海域和太平洋地区举行联合演习,我军自主演习时军舰A测得潜艇C的俯角为30°,位于军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5,$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
俄罗斯和中国2015年将在地中海海域和太平洋地区举行联合演习,我军自主演习时军舰A测得潜艇C的俯角为30°,位于军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5,$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)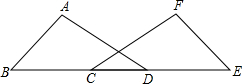 如图,在△ABD和△FEC中,点B,C,D,E在同一直线上,且AB=FE,BC=DE,∠B=∠E.求证:∠A=∠F.
如图,在△ABD和△FEC中,点B,C,D,E在同一直线上,且AB=FE,BC=DE,∠B=∠E.求证:∠A=∠F. 如图1,在△ABC中,AB=AC,BD是△ABC的高,P是BC边上一点,PN分别与直线AB,AC垂直,垂足分别为点M,N,求证:BD=PM+PN.
如图1,在△ABC中,AB=AC,BD是△ABC的高,P是BC边上一点,PN分别与直线AB,AC垂直,垂足分别为点M,N,求证:BD=PM+PN.