题目内容
某市自来水公司为了鼓励市民节约用水,于2014年4月开始采用以用户为单位按月分段收费办法收取水费,新按月分段收费标准如下:
标准一:每月用水不超过20吨(包括20吨)的水量,每吨收费2.45元;
标准二:每月用水超过20吨但不超过30吨的水量,按每吨a元收费;
标准三:超过30吨的部分,按每吨(a+1.62)元收费.(说明:a>2.45).
(1)居民甲4月份用水25吨,交水费65.4元,求a的值;
(2)若居民甲2014年4月以后,每月用水x(吨),应交水费y(元),求y与x之间的函数关系式,并注明自变量x的取值范围;
(3)随着夏天的到来,各家的用水量在不但增加.为了节省开支,居民甲计划自家6月份的水费不能超过家庭月收入的2%(居民甲家的月收入为6540元),则居民甲家六月份最多能用水多少吨?
标准一:每月用水不超过20吨(包括20吨)的水量,每吨收费2.45元;
标准二:每月用水超过20吨但不超过30吨的水量,按每吨a元收费;
标准三:超过30吨的部分,按每吨(a+1.62)元收费.(说明:a>2.45).
(1)居民甲4月份用水25吨,交水费65.4元,求a的值;
(2)若居民甲2014年4月以后,每月用水x(吨),应交水费y(元),求y与x之间的函数关系式,并注明自变量x的取值范围;
(3)随着夏天的到来,各家的用水量在不但增加.为了节省开支,居民甲计划自家6月份的水费不能超过家庭月收入的2%(居民甲家的月收入为6540元),则居民甲家六月份最多能用水多少吨?
考点:一次函数的应用,一元一次方程的应用,一元一次不等式的应用
专题:
分析:(1)由前20吨水的费用+超过20吨的水费建立方程求出其解即可;
(2)根据分段函数求解的方法当0≤x≤20时,当20<x≤30时,当x>30时分别由总费用=单价×数量就可以求出结论;
(3)先求出前30吨水费,再求出用于缴水费的费用,确定甲用水量的范围,再建立不等式求出其解即可.
(2)根据分段函数求解的方法当0≤x≤20时,当20<x≤30时,当x>30时分别由总费用=单价×数量就可以求出结论;
(3)先求出前30吨水费,再求出用于缴水费的费用,确定甲用水量的范围,再建立不等式求出其解即可.
解答:解:(1)由题意得,
20×2.45+5a=65.4
解之得,a=3.28;
(2)由题意得
当0≤x≤20时,y=2.45x;
当20<x≤30时,y=20×2.45+3.28(x-20)=3.28x-16.6;
当x>30时,y=20×2.45+10×3.28+(x-30)×(3.28+1.62)=4.9x-65.2,
∴y=
;
(3)由题意,得
6540×2%=130.8.
∵20×2.45=49;49+10×3.28=81.8
∵49<81.8<130.8,
∴居民甲家6月份用水超过30吨,设他家6月用水m吨,得,4.9m-65.2≤130.8,
解得m≤40.
答:居民甲家计划6月份最多用水40吨.
20×2.45+5a=65.4
解之得,a=3.28;
(2)由题意得
当0≤x≤20时,y=2.45x;
当20<x≤30时,y=20×2.45+3.28(x-20)=3.28x-16.6;
当x>30时,y=20×2.45+10×3.28+(x-30)×(3.28+1.62)=4.9x-65.2,
∴y=
|
(3)由题意,得
6540×2%=130.8.
∵20×2.45=49;49+10×3.28=81.8
∵49<81.8<130.8,
∴居民甲家6月份用水超过30吨,设他家6月用水m吨,得,4.9m-65.2≤130.8,
解得m≤40.
答:居民甲家计划6月份最多用水40吨.
点评:本题考查了一元一次方程的运用,一次函数的运用,一元一次不等式的运用,分类讨论思想的运用,解答时求出一次函数的解析式是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在Rt△ABC中,∠C=90°,sinA=
,AB=5,则边AC的长是( )
| 3 |
| 4 |
| A、3 | ||||
B、
| ||||
C、
| ||||
| D、4 |
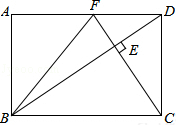 在矩形ABCD中,DC=
在矩形ABCD中,DC=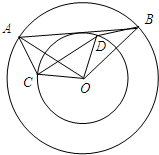 如图,两个同心圆的圆心为O,两圆的半径分别为5,3,其中A,B两点在大圆上,C,D在小圆上,且∠AOB=∠COD.
如图,两个同心圆的圆心为O,两圆的半径分别为5,3,其中A,B两点在大圆上,C,D在小圆上,且∠AOB=∠COD. (1)计算:2sin60°+2-1-20130-|1-
(1)计算:2sin60°+2-1-20130-|1-