题目内容
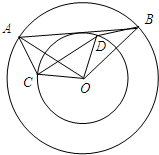 如图,两个同心圆的圆心为O,两圆的半径分别为5,3,其中A,B两点在大圆上,C,D在小圆上,且∠AOB=∠COD.
如图,两个同心圆的圆心为O,两圆的半径分别为5,3,其中A,B两点在大圆上,C,D在小圆上,且∠AOB=∠COD.(1)求证:AC=BD;
(2)若∠AOB=120°,求线段AC,弧CD,线段BD,弧AB组成的封闭图形的面积;
(3)若AB与小圆相切,分别求AB,CD的长.
考点:切线的性质,全等三角形的判定与性质,勾股定理,相似三角形的判定与性质
专题:
分析:(1)如要证明AC=BD,则通过可证明△AOC≌△BOD即可;
(2)由题意可知线段AC,弧CD,线段BD,弧AB组成的封闭图形的面积,即为扇形AOB的面积,即为△ACO绕O旋转120度后,AC扫过的面积;
(3)切点为E,连接OE,首先利用勾股定理可求出BE的长,进而求出AB的长,再证明△AOB∽△COD,利用相似三角形的性质即可求出CD的长.
(2)由题意可知线段AC,弧CD,线段BD,弧AB组成的封闭图形的面积,即为扇形AOB的面积,即为△ACO绕O旋转120度后,AC扫过的面积;
(3)切点为E,连接OE,首先利用勾股定理可求出BE的长,进而求出AB的长,再证明△AOB∽△COD,利用相似三角形的性质即可求出CD的长.
解答:(1)证明:在△AOC和△BOD中,
∵∠AOB=∠COD,
∴∠AOC=∠BOD,
∵OA=OB,OC=OD,
在△AOC和△BOD中,
,
∴△AOC≌△BOD(SAS),
∴AC=BD;
(2)解:封闭图形的面积=
×16π=
.
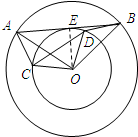 (3)解:设切点为E,连接OE,
(3)解:设切点为E,连接OE,
∵AB与小圆相切,
∴OE⊥AB,AB=2BE
由勾股定理得,BE=4,
∴AB=8.
∵∠AOB=∠COD,
=
,
∴△AOB∽△COD,
∴
=
=
∴CD=
.
∵∠AOB=∠COD,
∴∠AOC=∠BOD,
∵OA=OB,OC=OD,
在△AOC和△BOD中,
|
∴△AOC≌△BOD(SAS),
∴AC=BD;
(2)解:封闭图形的面积=
| 120 |
| 360 |
| 16π |
| 3 |
 (3)解:设切点为E,连接OE,
(3)解:设切点为E,连接OE,∵AB与小圆相切,
∴OE⊥AB,AB=2BE
由勾股定理得,BE=4,
∴AB=8.
∵∠AOB=∠COD,
| OA |
| OC |
| OB |
| OD |
∴△AOB∽△COD,
∴
| AB |
| CD |
| OA |
| OC |
| 5 |
| 3 |
∴CD=
| 24 |
| 5 |
点评:本题考查了全等三角形的判定和性质、切线的性质、垂径定理、勾股定理的运用以及相似三角形的判定和性质,题目的综合性较强,难度中等.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 在平面直角坐标系xOy中,二次函数y=2x2+bx+c的图象经过(-1,0)和(
在平面直角坐标系xOy中,二次函数y=2x2+bx+c的图象经过(-1,0)和( 生物学家为了推测最适合某种珍奇植物生长的温度时,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况(如下表).
生物学家为了推测最适合某种珍奇植物生长的温度时,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况(如下表).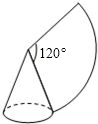 如图,用圆心角为120°半径为6的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的高是
如图,用圆心角为120°半径为6的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的高是