题目内容
在Rt△ABC中，∠C=90°，sinA=
，AB=5，则边AC的长是（ ）
| 3 |
| 4 |
| A、3 | ||||
B、
| ||||
C、
| ||||
| D、4 |
考点：解直角三角形
专题：计算题
分析：先根据正弦的定义得到sinA=
=
，则可设BC=3x，AB=4x，根据勾股定理得到AC=
x，再利用AB的长为5得到x=
，所以AC=
．
| BC |
| AB |
| 3 |
| 4 |
| 7 |
| 5 |
| 4 |
5
| ||
| 4 |
解答：解：∵sinA=
=
，
∴设BC=3x，AB=4x，
∴AC=
=
x，
∵4x=5，
∴x=
，
∴AC=
．
故选B．
| BC |
| AB |
| 3 |
| 4 |
∴设BC=3x，AB=4x，
∴AC=
| AB2-BC2 |
| 7 |
∵4x=5，
∴x=
| 5 |
| 4 |
∴AC=
5
| ||
| 4 |
故选B．
点评：本题考查了解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．
练习册系列答案
相关题目
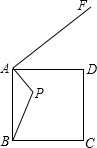已知点P是边长为5的正方形ABCD内一点，且AP=2，AF⊥AP，垂足是点A，若在射线AF上找一点M，使以点A，M，D为顶点的三角形与△ABP相似，则AM为（ ）| A、2 | ||
| B、5 | ||
C、2或
| ||
D、2或
|
下列说法正确的是（ ）
A、
| ||||||||
B、（
| ||||||||
C、
| ||||||||
D、
|
数据1，2，3的方差等于（ ）
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
对于正数x，规定f（x）=
，例如f（3）=
=
，f（
）=
=
，计算f（
）+f（
）+f（
）+…+f（
）+f（
）+f（1）+f（2）+f（3）+…+f（2012）+f（2013）+f（2014）的结果是（ ）
| x |
| 1+x |
| 3 |
| 1+3 |
| 3 |
| 4 |
| 1 |
| 3 |
| ||
1+
|
| 1 |
| 4 |
| 1 |
| 2014 |
| 1 |
| 2013 |
| 1 |
| 2012 |
| 1 |
| 3 |
| 1 |
| 2 |
| A、2013 |
| B、2013.5 |
| C、2014 |
| D、2014.5 |
在2、1、0、-1这四个数中，小于0的数是（ ）
| A、0 | B、-1 | C、1 | D、2 |
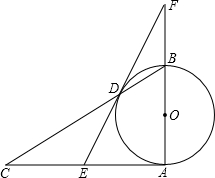已知：如图，在Rt△ABC中，∠A=90°，以AB为直径作⊙O，BC交⊙O于点D，E是边AC的中点，ED、AB的延长线相交于点F．