题目内容
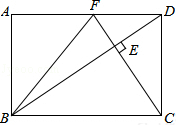 在矩形ABCD中,DC=
在矩形ABCD中,DC=| 6 |
(1)求证:△DEC∽△FDC;
(2)当F为AD的中点时,求sin∠FBD的值及BC的长度.
考点:矩形的性质,勾股定理,相似三角形的判定与性质
专题:
分析:(1)根据矩形性质和垂直定义得出∠DEC=∠FDC=90°,根据相似三角形的判定定理推出即可;
(2)求出FE:EC=FD:BC=1:2,FB=FC,推出FE:FC=1:3,求出sin∠FBD=EF:BF=EF:FC=
;设EF=x,则FC=3x,x=1,根据相似求出x=1,求出CF,根据勾股定理求出DF即可.
(2)求出FE:EC=FD:BC=1:2,FB=FC,推出FE:FC=1:3,求出sin∠FBD=EF:BF=EF:FC=
| 1 |
| 3 |
解答:证明:(1)∵四边形ABCD是矩形,
∴∠FDC=90°,
∵CF⊥BD,
∴∠DEC=∠FDC=90°,
∵∠DCE=∠FCD,
∴△DEC∽△FDC.
(2)解:∵F为AD的中点,AD∥BC,
∴FE:EC=FD:BC=1:2,FB=FC,
∴FE:FC=1:3,
∴sin∠FBD=EF:BF=EF:FC=
;
设EF=x,则FC=3x,
∵△DEC∽△FDC,
∴
=
,即可得:6x2=6,
解得:x=1,
则CF=3,
在Rt△CFD中,DF=
=
,
∴BC=2DF=2
.
∴∠FDC=90°,
∵CF⊥BD,
∴∠DEC=∠FDC=90°,
∵∠DCE=∠FCD,
∴△DEC∽△FDC.
(2)解:∵F为AD的中点,AD∥BC,
∴FE:EC=FD:BC=1:2,FB=FC,
∴FE:FC=1:3,
∴sin∠FBD=EF:BF=EF:FC=
| 1 |
| 3 |
设EF=x,则FC=3x,
∵△DEC∽△FDC,
∴
| CE |
| CD |
| CD |
| FC |
解得:x=1,
则CF=3,
在Rt△CFD中,DF=
| FC2-CD2 |
| 3 |
∴BC=2DF=2
| 3 |
点评:本题考查了矩形的性质,勾股定理,相似三角形的性质和判定的应用,主要考查学生运用定理进行推理和计算的能力.

练习册系列答案
相关题目
数据1,2,3的方差等于( )
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
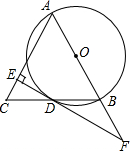 如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作EF⊥AC,垂足为E,交AB的延长线于点F.
如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作EF⊥AC,垂足为E,交AB的延长线于点F. 如图,已知四边形ABFC为菱形,点 D、A、E在直线l上,∠BDA=∠BAC=∠CEA.
如图,已知四边形ABFC为菱形,点 D、A、E在直线l上,∠BDA=∠BAC=∠CEA.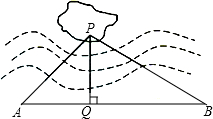 如图,某湖中有一孤立的小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PQ通往小岛,某同学在观光道AB上测得如下数据:AB=100米,∠PAB=45°,∠PBA=30.请求出小桥PQ的长.(
如图,某湖中有一孤立的小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PQ通往小岛,某同学在观光道AB上测得如下数据:AB=100米,∠PAB=45°,∠PBA=30.请求出小桥PQ的长.(