题目内容
11.如果两个相似三角形的相似比是1:$\sqrt{2}$,那么这两个相似三角形的面积比是( )| A. | 2:1 | B. | 1:$\sqrt{2}$ | C. | 1:2 | D. | 1:4 |
分析 直接根据似三角形的面积的比等于相似比的平方进行计算即可.
解答 解:这两个相似三角形的面积比=12:($\sqrt{2}$)2=1:2.
故选C.
点评 本题考查了相似三角形的性质:相似三角形的对应角相等,对应边的比相等;相似三角形的周长的比等于相似比;相似三角形的面积的比等于相似比的平方.

练习册系列答案
相关题目
2.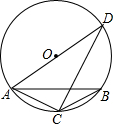 如图,AD是⊙O的直径,∠ACB=120°,$\widehat{AC}$=$\widehat{BC}$,BC=2$\sqrt{3}$,则DC的长是( )
如图,AD是⊙O的直径,∠ACB=120°,$\widehat{AC}$=$\widehat{BC}$,BC=2$\sqrt{3}$,则DC的长是( )
 如图,AD是⊙O的直径,∠ACB=120°,$\widehat{AC}$=$\widehat{BC}$,BC=2$\sqrt{3}$,则DC的长是( )
如图,AD是⊙O的直径,∠ACB=120°,$\widehat{AC}$=$\widehat{BC}$,BC=2$\sqrt{3}$,则DC的长是( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 6 |
16.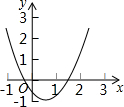 如图是二次函数y=ax2+bx+c(a≠0)在平面直角坐标系中的图象,根据图形判断①b>0;②a-b+c<0;③2a+b>0;④b2+8a>4ac中正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)在平面直角坐标系中的图象,根据图形判断①b>0;②a-b+c<0;③2a+b>0;④b2+8a>4ac中正确的是( )
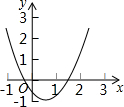 如图是二次函数y=ax2+bx+c(a≠0)在平面直角坐标系中的图象,根据图形判断①b>0;②a-b+c<0;③2a+b>0;④b2+8a>4ac中正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)在平面直角坐标系中的图象,根据图形判断①b>0;②a-b+c<0;③2a+b>0;④b2+8a>4ac中正确的是( )| A. | ①② | B. | ①③ | C. | ③④ | D. | ②④ |
3.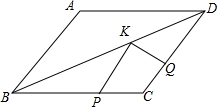 如图,△ABD≌△CDB,且∠ADB=∠ABD,△ABD的面积是2$\sqrt{3}$,AB=2,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
如图,△ABD≌△CDB,且∠ADB=∠ABD,△ABD的面积是2$\sqrt{3}$,AB=2,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
 如图,△ABD≌△CDB,且∠ADB=∠ABD,△ABD的面积是2$\sqrt{3}$,AB=2,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
如图,△ABD≌△CDB,且∠ADB=∠ABD,△ABD的面积是2$\sqrt{3}$,AB=2,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )| A. | $\sqrt{3}$ | B. | 4 | C. | 2 | D. | 2$\sqrt{3}$ |
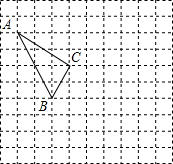 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).