题目内容
16.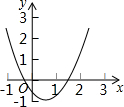 如图是二次函数y=ax2+bx+c(a≠0)在平面直角坐标系中的图象,根据图形判断①b>0;②a-b+c<0;③2a+b>0;④b2+8a>4ac中正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)在平面直角坐标系中的图象,根据图形判断①b>0;②a-b+c<0;③2a+b>0;④b2+8a>4ac中正确的是( )| A. | ①② | B. | ①③ | C. | ③④ | D. | ②④ |
分析 首先根据图象中抛物线的开口方向、对称轴的位置、与y轴交点来判断a、b、c的符号,进而判断各结论是否正确.
解答 解:根据二次函数的图象知:抛物线开口向上,则a>0;
抛物线的对称轴在y轴右侧,则x=-$\frac{b}{2a}$>0,即b<0,故①错误;
由图知:当x=-1时,y>0;即a-b+c>0,故②错误;
由对称轴-$\frac{b}{2a}$<1可知:2a>-b,所以2a+b>0,故③正确;
∵抛物线交y轴于负半轴,∴c<0,
∵由于抛物线与x轴有两个不同的交点,∴△=b2-4ac>0,即b2>4ac;
∵a>0,∴8a>0;
∴b2+8a>4ac,故④正确;
所以正确的结论为③④,
故选C.
点评 本题考查了二次函数图象与系数的关系,由图象找出有关a,b,c的相关信息以及抛物线的交点坐标,会利用特殊值代入法求得特殊的式子,如:y=a+b+c,y=a-b+c,然后根据图象判断其值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
7.将4cm长的线段分成两部分,一部分作为正方形的一条边,另一部分作为一个等腰直角三角形的斜边,则这个正方形和等腰直角三角形的面积之和的最小值为( )cm2.
| A. | 1 | B. | $\frac{4}{5}$ | C. | 16 | D. | $\frac{16}{5}$ |
11.如果两个相似三角形的相似比是1:$\sqrt{2}$,那么这两个相似三角形的面积比是( )
| A. | 2:1 | B. | 1:$\sqrt{2}$ | C. | 1:2 | D. | 1:4 |
1.已知a<b,则下列各式不成立的是( )
| A. | 4a<4b | B. | -4a<-4b | C. | a-4<b-4 | D. | 4+a<4+b |