题目内容
2.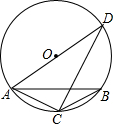 如图,AD是⊙O的直径,∠ACB=120°,$\widehat{AC}$=$\widehat{BC}$,BC=2$\sqrt{3}$,则DC的长是( )
如图,AD是⊙O的直径,∠ACB=120°,$\widehat{AC}$=$\widehat{BC}$,BC=2$\sqrt{3}$,则DC的长是( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 6 |
分析 如图,连接OC.根据圆周角、弧、弦的关系可以判定AC=BC=2$\sqrt{3}$,利用勾股定理来求CD的长度即可.
解答  解:如图,连接OC.
解:如图,连接OC.
∵$\widehat{AC}$=$\widehat{BC}$,
∴点C是$\widehat{AB}$的中点,AC=BC=2$\sqrt{3}$,∠ACO=∠BCO=$\frac{1}{2}$∠ACB=60°.
又∵OA=OC,
∴△OAC是等边三角形,
∴∠OAC=60°,
又∵AD是⊙O的直径,
∴∠ACD=90°,
∴CD=AC•tan60°=2$\sqrt{3}$×$\sqrt{3}$=6.
故选:D.
点评 本题考查了圆周角定理,圆周角、弧、弦的关系.根据题意推知△OAC是等边三角形是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
7.将4cm长的线段分成两部分,一部分作为正方形的一条边,另一部分作为一个等腰直角三角形的斜边,则这个正方形和等腰直角三角形的面积之和的最小值为( )cm2.
| A. | 1 | B. | $\frac{4}{5}$ | C. | 16 | D. | $\frac{16}{5}$ |
11.如果两个相似三角形的相似比是1:$\sqrt{2}$,那么这两个相似三角形的面积比是( )
| A. | 2:1 | B. | 1:$\sqrt{2}$ | C. | 1:2 | D. | 1:4 |
