题目内容
19.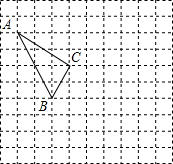 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△DEF,其中点A对应点D,点B对应点E,点C对应点F;
(3)写出点E关于原点的对称点M的坐标.
分析 (1)根据题意画出坐标系即可;
(2)根据关于y轴对称的点的坐标特点作出△DEF即可;
(3)根据中心对称的特点直接写出答案即可.
解答 解:(1)(2)如图:
(3)根据图象得到点E的坐标为(2,1),其关于原点对称的点的坐标为(-2,-1).
点评 本题考查的是作图-轴对称变换,熟知关于y轴对称的点的坐标特点是解答此题的关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
9.计算(-$\frac{1}{7}$)-3的结果是( )
| A. | -$\frac{1}{343}$ | B. | -$\frac{1}{21}$ | C. | -343 | D. | -21 |
7.将4cm长的线段分成两部分,一部分作为正方形的一条边,另一部分作为一个等腰直角三角形的斜边,则这个正方形和等腰直角三角形的面积之和的最小值为( )cm2.
| A. | 1 | B. | $\frac{4}{5}$ | C. | 16 | D. | $\frac{16}{5}$ |
11.如果两个相似三角形的相似比是1:$\sqrt{2}$,那么这两个相似三角形的面积比是( )
| A. | 2:1 | B. | 1:$\sqrt{2}$ | C. | 1:2 | D. | 1:4 |
9.若a0、b0都是单位向量,则有( )
| A. | a0=b0 | B. | a0=-b0 | C. | |a0|=|b0| | D. | a0=±b0 |
