题目内容
3.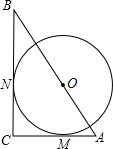 如图,△ABC中,∠C=90°,⊙O分别切AC,BC于点M,N,圆心O在AB上,且AO=15cm,BO=20cm,求⊙O的面积.
如图,△ABC中,∠C=90°,⊙O分别切AC,BC于点M,N,圆心O在AB上,且AO=15cm,BO=20cm,求⊙O的面积.
分析 设⊙O的半径为r,连接ON、OM,由切线的性质可知ON⊥BC,则ON∥AC,且ON=OM=r,在Rt△BON中,可用r表示出BN,利用平行线分线段成比例可得到关于r的方程,可求得r,是可求得⊙O的面积.
解答 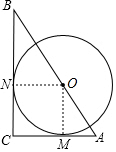 解:
解:
设⊙O的半径为r,连接ON、OM,
∵⊙O分别切AC,BC于点M,N,
∴ON⊥BC,OM⊥AC,且OM=ON=r,∠C=90°,
∴四边形OMCN为正方形,
∴CN=OM=r,
∴ON∥AC,
∴$\frac{BN}{CN}$=$\frac{BO}{AO}$,即$\frac{BN}{r}$=$\frac{20}{15}$,
∴BN=$\frac{4}{3}$r,
在Rt△BON中,由勾股定理可得ON2+BN2=BO2,
∴r2+($\frac{4}{3}$r)2=202,解得r=12,
∴S圆O=πr2=144π.
点评 本题主要考查切线的性质及圆的面积,作出过切点半构造出正方形,利用平行线分线段成比例求得圆的半径是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.对于(-3)5,下列说法错误的是( )
| A. | (-3)5>(-5)3 | B. | 其结果一定是负数 | ||
| C. | 其结果与-35 相同 | D. | 表示5个-3相乘 |
 如图,四边形ABCD是平行四边形,且AB=AC,过A,B,C三点的⊙O与DC的延长线交于点E,连接AE交BC于F.
如图,四边形ABCD是平行四边形,且AB=AC,过A,B,C三点的⊙O与DC的延长线交于点E,连接AE交BC于F. 二次函数y=-x2+bx+c的图象如图所示,则该二次函数的函数关系式为y=-x2+2x+3.
二次函数y=-x2+bx+c的图象如图所示,则该二次函数的函数关系式为y=-x2+2x+3.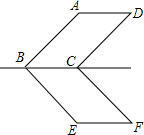 如图,?ABCD与?EBCF关于BC所在直线对称,∠ABE=90°,求∠F.
如图,?ABCD与?EBCF关于BC所在直线对称,∠ABE=90°,求∠F. 如图,AB∥CD∥EF,猜想:∠1、∠2、∠3之间的数量关系是∠1-∠2+∠3=180°,请证之.
如图,AB∥CD∥EF,猜想:∠1、∠2、∠3之间的数量关系是∠1-∠2+∠3=180°,请证之.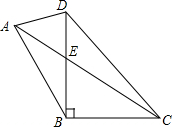 如图,在四边形ABCD中,∠DBC=90°,∠ABD=30°,∠ADB=75°,AC与BD交于点E,若CE=2AE=4$\sqrt{3}$,则DC的长为6$\sqrt{2}$.
如图,在四边形ABCD中,∠DBC=90°,∠ABD=30°,∠ADB=75°,AC与BD交于点E,若CE=2AE=4$\sqrt{3}$,则DC的长为6$\sqrt{2}$. 如图所示,经过圆内一点P作弦AB和CD,且DP=BP,求证:PA=PC.
如图所示,经过圆内一点P作弦AB和CD,且DP=BP,求证:PA=PC.