题目内容
18．
二次函数y=-x2+bx+c的图象如图所示，则该二次函数的函数关系式为y=-x2+2x+3．
分析 根据对称轴为直线x=1得出b，再把（3，0）代入即可得出c，从而得出二次函数的表达式．
解答 解：∵对称轴为直线x=1，
∴b=2，
把（3，0）代入y=-x2+2x+c得c=3，
∴二次函数的表达式为y=-x2+2x+3，
故答案为y=-x2+2x+3．
点评 本题考查了用待定系数法求二次函数的解析式，根据图象得出b和c的值是解题的关键．
练习册系列答案
相关题目
8．在同样条件下对某种小麦种子进行发芽试验，统计发芽种子数，获得如下频数表．
（1）计算表中a，b的值；
（2）估计该麦种的发芽概率；
（3）如果该麦种发芽后，只有87%的麦芽可以成活，现有100kg麦种，则有多少千克的麦种可以成活为秧苗？
| 试验种子n（粒） | 1 | 5 | 50 | 100 | 200 | 500 | 1000 | 2000 | 3000 |
| 发芽频数m | 1 | 4 | 45 | 92 | 188 | 476 | 951 | 1900 | 2850 |
| 发芽频率$\frac{m}{n}$ | 0 | 0.80 | 0.90 | 0.92 | 0.94 | 0.952 | 0.951 | a | b |
（2）估计该麦种的发芽概率；
（3）如果该麦种发芽后，只有87%的麦芽可以成活，现有100kg麦种，则有多少千克的麦种可以成活为秧苗？
9．二次函数y=x2+4x+3的图象可以由二次函数y=x2的图象平移而得到，下列平移正确的是（ ）
| A． | 先向左平移2个单位，再向下平移1个单位 | |
| B． | 先向左平移2个单位，再向上平移1个单位 | |
| C． | 先向右平移2个单位，再向下平移1个单位 | |
| D． | 先向右平移2个单位，再向上平移1个单位 |
13．抛物线y=ax2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表：
从上表可知，下列说法中正确的是（ ）
①抛物线与x轴的一个交点为（3，0）；
②函数y=ax2+bx+c的最大值为6；
③抛物线的对称轴是直线x=$\frac{1}{2}$；
④在对称轴左侧，y随x增大而增大．
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
①抛物线与x轴的一个交点为（3，0）；
②函数y=ax2+bx+c的最大值为6；
③抛物线的对称轴是直线x=$\frac{1}{2}$；
④在对称轴左侧，y随x增大而增大．
| A． | ①②③ | B． | ①③④ | C． | ①②④ | D． | ②③④ |
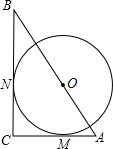如图，△ABC中，∠C=90°，⊙O分别切AC，BC于点M，N，圆心O在AB上，且AO=15cm，BO=20cm，求⊙O的面积．
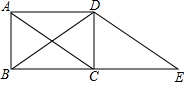如图，四边形ABCD是矩形，DE∥AC且交BC的延长线于点E，判断△DBE的形状，并证明你的结论．