题目内容
2. 如图所示,经过圆内一点P作弦AB和CD,且DP=BP,求证:PA=PC.
如图所示,经过圆内一点P作弦AB和CD,且DP=BP,求证:PA=PC.
分析 连接BD,如图,利用等腰三角形的性质得∠B=∠D,再利用圆周角定理得到$\widehat{BC}$=$\widehat{DA}$,则$\widehat{AB}$=$\widehat{CD}$,然后根据圆心角、弧、弦的关系得到BA=CD,所以AP=CP.
解答 证明:连接BD,如图,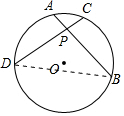
∵DP=BP
∴∠B=∠D,
∴$\widehat{BC}$=$\widehat{DA}$,
∴$\widehat{AB}$=$\widehat{CD}$,
∴BA=DC,
∴AP=CP.
点评 本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.

练习册系列答案
相关题目
13.如图,两个形状、大小完全相同的大长方形内放入四个如图③的小长方形后分别得到如图①、图②,已知大长方形的长为a,则图②阴影部分周长与图①阴影部分周长的差是( )
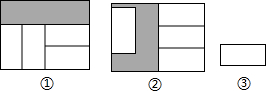

| A. | a | B. | $\frac{a}{3}$ | C. | $\frac{2}{3}$a | D. | $\frac{a}{2}$ |
10. 四边形ABCD两条对角线AC、BD互相垂直,AC+BD=20,则四边形ABCD的面积不能是( )
四边形ABCD两条对角线AC、BD互相垂直,AC+BD=20,则四边形ABCD的面积不能是( )
 四边形ABCD两条对角线AC、BD互相垂直,AC+BD=20,则四边形ABCD的面积不能是( )
四边形ABCD两条对角线AC、BD互相垂直,AC+BD=20,则四边形ABCD的面积不能是( )| A. | 55 | B. | 50 | C. | 45 | D. | 40 |
14.一次函数y=mx+|m-1|的图象过点(0,2),且y随x的增大而减小,则m的值为( )
| A. | -1 | B. | 1 | C. | 3 | D. | -1或3 |
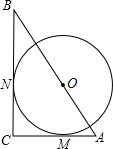 如图,△ABC中,∠C=90°,⊙O分别切AC,BC于点M,N,圆心O在AB上,且AO=15cm,BO=20cm,求⊙O的面积.
如图,△ABC中,∠C=90°,⊙O分别切AC,BC于点M,N,圆心O在AB上,且AO=15cm,BO=20cm,求⊙O的面积. 如图,P是∠α的边OA上一点,且点P的坐标为(1,$\sqrt{7}$),则sinα=$\frac{\sqrt{14}}{4}$.
如图,P是∠α的边OA上一点,且点P的坐标为(1,$\sqrt{7}$),则sinα=$\frac{\sqrt{14}}{4}$.