题目内容
14. 如图,四边形ABCD是平行四边形,且AB=AC,过A,B,C三点的⊙O与DC的延长线交于点E,连接AE交BC于F.
如图,四边形ABCD是平行四边形,且AB=AC,过A,B,C三点的⊙O与DC的延长线交于点E,连接AE交BC于F.(1)求证:AD是⊙O的切线;
(2)求证:△DAC∽△DEA.
分析 (1)连接OA,根据AB=AC,点A,B,C三点在⊙O上,可得OA垂直平分BC,根据四边形ABCD是平行四边形,得OA⊥AD,即AD是⊙O的切线;
(2)根据AB=AC,∠DEA=∠BCA,再由AD∥BC,得∠DAC=∠BCA,从而得出∠DEA=∠DAC,可证△DAC∽△DEA.
解答 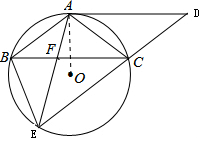 解:(1)连接OA,
解:(1)连接OA,
∵AB=AC,点A,B,C三点在⊙O上,
∴OA垂直平分BC,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴OA⊥AD,
∴AD是⊙O的切线;
(2)∵AB=AC,
∴∠DEA=∠BCA,
∵AD∥BC,
∴∠DAC=∠BCA,
∴∠DEA=∠DAC,
∵∠D=∠D,
∴△DAC∽△DEA.
点评 本题考查了相似三角形的判定以及平行四边形的性质、切线的判定,掌握判定定理是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
2.用加减消元法解二元一次方程组$\left\{\begin{array}{l}{2x-3y=7①}\\{5x-3y=-2②}\end{array}\right.$,由①-②可得的方程为( )
| A. | 3x=5 | B. | -3x=9 | C. | -3x-6y=9 | D. | 3x-6y=5 |
9.二次函数y=x2+4x+3的图象可以由二次函数y=x2的图象平移而得到,下列平移正确的是( )
| A. | 先向左平移2个单位,再向下平移1个单位 | |
| B. | 先向左平移2个单位,再向上平移1个单位 | |
| C. | 先向右平移2个单位,再向下平移1个单位 | |
| D. | 先向右平移2个单位,再向上平移1个单位 |
13.如图,两个形状、大小完全相同的大长方形内放入四个如图③的小长方形后分别得到如图①、图②,已知大长方形的长为a,则图②阴影部分周长与图①阴影部分周长的差是( )
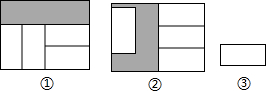

| A. | a | B. | $\frac{a}{3}$ | C. | $\frac{2}{3}$a | D. | $\frac{a}{2}$ |
 如图,∠C=20°,则∠AOB=40°.
如图,∠C=20°,则∠AOB=40°. 如图,AB为⊙O的直径,ED切⊙O于点C,过点A作AF⊥ED于点F,交⊙O于点G,连接AC;
如图,AB为⊙O的直径,ED切⊙O于点C,过点A作AF⊥ED于点F,交⊙O于点G,连接AC;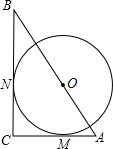 如图,△ABC中,∠C=90°,⊙O分别切AC,BC于点M,N,圆心O在AB上,且AO=15cm,BO=20cm,求⊙O的面积.
如图,△ABC中,∠C=90°,⊙O分别切AC,BC于点M,N,圆心O在AB上,且AO=15cm,BO=20cm,求⊙O的面积.