题目内容
10.某学校为了检测学生的学习能力,设计了一份测试卷,要求检测对象在45分钟内学习特定的材料,并解答相关问题(满分100分).已知被测试者的学习能力指标P与其所得分数x(分)和完成所需时间t(分钟)存在函数关系:p=ktx2+mx.在检测过程中得到如下数据:| 检测成绩x(分) | 完成时间t(分钟) | 学习能力指标p | |
| 1 | 100 | 30 | 90 |
| 2 | 100 | 40 | 80 |
(2)小红用了35分钟完成了该项测试,其成绩为80分,试确定其学习能力指标P的值;
(3)小红用了25分钟完成了该项检测,要使小兵的学习能力指标P取最大值,他检测成绩应该是多少分?
分析 (1)根据待定系数法可求k和m的值;
(2)代值计算即可求解;
(3)先配方,根据二次函数的最值即可求解.
解答 解:(1)依题意有$\left\{\begin{array}{l}{30×10{0}^{2}k+100m=90}\\{40×10{0}^{2}k+100m=80}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-0.0001}\\{m=0.6}\end{array}\right.$;
(2)p=ktx2+mx=-0.0001tx2+0.6x,
∵t=35,x=80,
∴p=-0.0001×35×802+0.6×80=25.6;
(3)p=-0.0001×25x2+0.6x=-0.0025x2+0.6x=-0.0025(x2-240x)=-0.0025(x-120)2+36
∵x≤100,
∴要使小兵的学习能力指标P取最大值,他检测成绩应该是100分.
点评 本题考查了二次函数的应用:先通过待定系数法确定二次函数关系式,然后给定自变量的值求出对应的函数值.

练习册系列答案
相关题目
11.在平面直角坐标系中,点P(m-3,4-2m)不可能在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
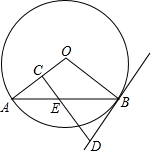 如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D.
如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D. 如图,在平面直角坐标系中,双曲线y=$\frac{k}{x}$与直线y=ax+b的交点A、B均在小正方形的顶点上,每个小正方形的边长均为1.
如图,在平面直角坐标系中,双曲线y=$\frac{k}{x}$与直线y=ax+b的交点A、B均在小正方形的顶点上,每个小正方形的边长均为1.