题目内容
12.计算:-(-2)+$\sqrt{8}$-2sin45°+(-1)3.分析 首先利用二次根式的性质以及特殊角的三角函数值分别化简得出答案.
解答 解:原式=2+2$\sqrt{2}$-2×$\frac{\sqrt{2}}{2}$-1
=1+$\sqrt{2}$.
点评 此题主要考查了实数运算,正确化简各数是解题关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
3.不等式组:$\left\{\begin{array}{l}x-2≤0\\ x+3>0\end{array}\right.$的解集是( )
| A. | -3<x≤2 | B. | -3≤x<2 | C. | x≥2 | D. | x<-3 |
7.桌面上放置的几何体中,主视图与左视图可能不同的是( )
| A. | 圆柱 | B. | 正方体 | C. | 球 | D. | 直立圆锥 |
17. 实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是( )
实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是( )
 实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是( )
实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是( )| A. | a>-4 | B. | bd>0 | C. | |a|>|d| | D. | b+c>0 |
10.某学校为了检测学生的学习能力,设计了一份测试卷,要求检测对象在45分钟内学习特定的材料,并解答相关问题(满分100分).已知被测试者的学习能力指标P与其所得分数x(分)和完成所需时间t(分钟)存在函数关系:p=ktx2+mx.在检测过程中得到如下数据:
(1)求k和m的值;
(2)小红用了35分钟完成了该项测试,其成绩为80分,试确定其学习能力指标P的值;
(3)小红用了25分钟完成了该项检测,要使小兵的学习能力指标P取最大值,他检测成绩应该是多少分?
| 检测成绩x(分) | 完成时间t(分钟) | 学习能力指标p | |
| 1 | 100 | 30 | 90 |
| 2 | 100 | 40 | 80 |
(2)小红用了35分钟完成了该项测试,其成绩为80分,试确定其学习能力指标P的值;
(3)小红用了25分钟完成了该项检测,要使小兵的学习能力指标P取最大值,他检测成绩应该是多少分?
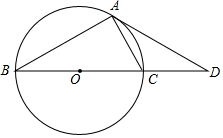 如图,已知BC是⊙O的直径,点D为BC延长线上的一点,点A为圆上一点,且AB=AD,AC=CD.
如图,已知BC是⊙O的直径,点D为BC延长线上的一点,点A为圆上一点,且AB=AD,AC=CD.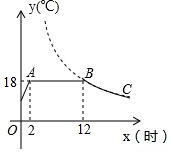 如图是某蔬菜大棚恒温系统从开启到关闭后,大棚内温度y(℃)随时间x(时)变化的函数图象,其中BC段是反比例函数图象的一部分,则当x=20时,大棚内的温度约为10.8℃.
如图是某蔬菜大棚恒温系统从开启到关闭后,大棚内温度y(℃)随时间x(时)变化的函数图象,其中BC段是反比例函数图象的一部分,则当x=20时,大棚内的温度约为10.8℃.