题目内容
5.小明的妈妈在菜市场买回1.5千克萝卜,1千克排骨,准备做萝卜排骨汤,下面是这一家三口的对话,请根据对话解决小明提出的问题.妈妈:“今天买这两样菜共花了45元,上月同质量的这两样菜只要36元”
爸爸:“报纸上说萝卜的单价比上月上涨了50%,排骨的单价比上月上涨了20%”
小明:“爸爸、妈妈,今天买的萝卜和排骨的单价分别是多少?”
分析 设上月萝卜的单价是x元/千克,排骨的单价y元/千克,根据小明的爸爸和妈妈的对话找到等量关系列出方程求解即可.
解答 解:设上月萝卜的单价是x元/千克,排骨的单价y元/千克,根据题意得
$\left\{\begin{array}{l}{1.5x+y=36}\\{1.5(1+50%)x+(1+20%)y=45}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=4}\\{y=30}\end{array}\right.$.
今天萝卜的单价是4×(1+50%)=6元/千克,排骨的单价是30×(1+20%)=36元/千克.
答:今天萝卜的单价是3元/千克,排骨的单价是18元/千克.
点评 本题考查了二元一次方程组的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程组,再求解.

练习册系列答案
相关题目
6.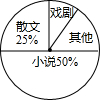 八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类型,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.
八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类型,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.
根据图表提供的信息,解答下列问题:
(1)八年级一班有多少名学生?
(2)请补全频数分布表,并求出扇形统计图中“其他”类所占的百分比;
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从以上四位同学中任意选出2名同学参加学校的戏剧兴趣小组,请用画树状图或列表法的方法,求选取的2人恰好是乙和丙的概率.
 八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类型,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.
八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类型,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.| 类别 | 频数(人数) | 频率 |
| 小说 | 0.5 | |
| 戏剧 | 4 | |
| 散文 | 10 | 0.25 |
| 其他 | 6 | |
| 合计 | 1 |
(1)八年级一班有多少名学生?
(2)请补全频数分布表,并求出扇形统计图中“其他”类所占的百分比;
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从以上四位同学中任意选出2名同学参加学校的戏剧兴趣小组,请用画树状图或列表法的方法,求选取的2人恰好是乙和丙的概率.
7.桌面上放置的几何体中,主视图与左视图可能不同的是( )
| A. | 圆柱 | B. | 正方体 | C. | 球 | D. | 直立圆锥 |
10.某学校为了检测学生的学习能力,设计了一份测试卷,要求检测对象在45分钟内学习特定的材料,并解答相关问题(满分100分).已知被测试者的学习能力指标P与其所得分数x(分)和完成所需时间t(分钟)存在函数关系:p=ktx2+mx.在检测过程中得到如下数据:
(1)求k和m的值;
(2)小红用了35分钟完成了该项测试,其成绩为80分,试确定其学习能力指标P的值;
(3)小红用了25分钟完成了该项检测,要使小兵的学习能力指标P取最大值,他检测成绩应该是多少分?
| 检测成绩x(分) | 完成时间t(分钟) | 学习能力指标p | |
| 1 | 100 | 30 | 90 |
| 2 | 100 | 40 | 80 |
(2)小红用了35分钟完成了该项测试,其成绩为80分,试确定其学习能力指标P的值;
(3)小红用了25分钟完成了该项检测,要使小兵的学习能力指标P取最大值,他检测成绩应该是多少分?
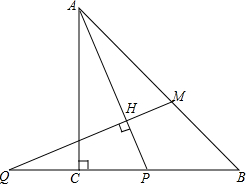 在等腰直角△ABC中,∠ACB=90°,P是线段BC上一动点(与点B、C不重合),连接AP,延长BC至点Q,使得CQ=CP,过点Q作QH⊥AP于点H,交AB于点M.
在等腰直角△ABC中,∠ACB=90°,P是线段BC上一动点(与点B、C不重合),连接AP,延长BC至点Q,使得CQ=CP,过点Q作QH⊥AP于点H,交AB于点M. 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(k≠0)与一次函数y=ax+b
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(k≠0)与一次函数y=ax+b