题目内容
15. 如图,在平面直角坐标系中,双曲线y=$\frac{k}{x}$与直线y=ax+b的交点A、B均在小正方形的顶点上,每个小正方形的边长均为1.
如图,在平面直角坐标系中,双曲线y=$\frac{k}{x}$与直线y=ax+b的交点A、B均在小正方形的顶点上,每个小正方形的边长均为1.(1)求k的值.
(2)把直线AB向右平移5个单位,再向上平移5个单位,画出每次平移后的直线.并求出平移后的直线的函数解析式.
分析 (1)根据图象可以得到A,B的坐标,把点A或点B代入双曲线y=$\frac{k}{x}$,可以求出k值.
(2)根据两点所在象限及距离坐标轴的距离可得相应坐标,进而把两点做相应的平移,连接即可得到平移后的直线;由图可得直线过(0,5)和(5,0),代入解析式解方程即可得到结论.
解答 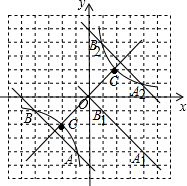 解:(1)由图可得点A的坐标为(-1,-4),
解:(1)由图可得点A的坐标为(-1,-4),
把(-1,-4)代入$y=\frac{k}{x}$中,-4=$\frac{k}{-1}$,
解得k=4;
(2)设平移后的直线为y=ax+c,由图可得直线过(0,5)和(5,0)
则$\left\{\begin{array}{l}c=5\\ 5a+c=0\end{array}\right.$可得$\left\{\begin{array}{l}c=5\\ a=-1\end{array}\right.$
∴平移后直线为y=-x+5.
点评 本题考查了反比例函数与一次函数的交点问题,平移变换作图及反比例函数的相关知识;平移时看关键点的平移即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17. 实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是( )
实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是( )
 实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是( )
实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是( )| A. | a>-4 | B. | bd>0 | C. | |a|>|d| | D. | b+c>0 |
10.某学校为了检测学生的学习能力,设计了一份测试卷,要求检测对象在45分钟内学习特定的材料,并解答相关问题(满分100分).已知被测试者的学习能力指标P与其所得分数x(分)和完成所需时间t(分钟)存在函数关系:p=ktx2+mx.在检测过程中得到如下数据:
(1)求k和m的值;
(2)小红用了35分钟完成了该项测试,其成绩为80分,试确定其学习能力指标P的值;
(3)小红用了25分钟完成了该项检测,要使小兵的学习能力指标P取最大值,他检测成绩应该是多少分?
| 检测成绩x(分) | 完成时间t(分钟) | 学习能力指标p | |
| 1 | 100 | 30 | 90 |
| 2 | 100 | 40 | 80 |
(2)小红用了35分钟完成了该项测试,其成绩为80分,试确定其学习能力指标P的值;
(3)小红用了25分钟完成了该项检测,要使小兵的学习能力指标P取最大值,他检测成绩应该是多少分?
20.观察下表:
我们把某格中字母和所得到的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y,回答下列问题:
(1)第3格的“特征多项式”为16x+9y,第4格的“特征多项式”为25x+16y,第n格的“特征多项式”为(n+1)2x+n2y;
(2)若第1格的“特征多项式”的值为-10,第2格的“特征多项式”的值为-16.
①求x,y的值;
②在①的条件下,第n格的“特征多项式”是否有最小值?若有,求出最小值和相应的n值;若没有,请说明理由.
我们把某格中字母和所得到的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y,回答下列问题:
| 序号 | 1 | 2 | 3 | … |
图形 | x x y x x | x x x y y x x x y y x x x | x x x x y y y x x x x y y y x x x x y y y x x x x | … |
(2)若第1格的“特征多项式”的值为-10,第2格的“特征多项式”的值为-16.
①求x,y的值;
②在①的条件下,第n格的“特征多项式”是否有最小值?若有,求出最小值和相应的n值;若没有,请说明理由.
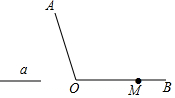 尺规作图(不写作法,保留作图痕迹):
尺规作图(不写作法,保留作图痕迹):