题目内容
9.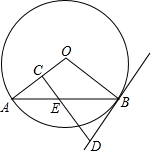 如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D.
如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D.(1)求证:DB=DE;
(2)若AB=12,BD=5,求⊙O的半径.
分析 (1)欲证明DB=DE,只要证明∠DEB=∠DBE;
(2)作DF⊥AB于F,连接OE.只要证明∠AOE=∠DEF,可得sin∠DEF=sin∠AOE=$\frac{AE}{AO}$=$\frac{4}{5}$,由此求出AE即可解决问题.
解答 (1)证明:∵AO=OB,
∴∠OAB=∠OBA,
∵BD是切线,
∴OB⊥BD,
∴∠OBD=90°,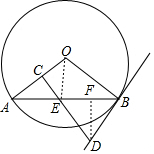
∴∠OBE+∠EBD=90°,
∵EC⊥OA,
∴∠CAE+∠CEA=90°,
∵∠CEA=∠DEB,
∴∠EBD=∠BED,
∴DB=DE.
(2)作DF⊥AB于F,连接OE.
∵DB=DE,AE=EB=6,
∴EF=$\frac{1}{2}$BE=3,OE⊥AB,
在Rt△EDF中,DE=BD=5,EF=3,
∴DF=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∵∠AOE+∠A=90°,∠DEF+∠A=90°,
∴∠AOE=∠DEF,
∴sin∠DEF=sin∠AOE=$\frac{AE}{AO}$=$\frac{4}{5}$,
∵AE=6,
∴AO=$\frac{15}{2}$.
∴⊙O的半径为$\frac{15}{2}$.
点评 本题考查切线的性质、勾股定理、垂径定理、锐角三角函数、等腰三角形的性质等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
17. 实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是( )
实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是( )
 实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是( )
实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是( )| A. | a>-4 | B. | bd>0 | C. | |a|>|d| | D. | b+c>0 |
10.某学校为了检测学生的学习能力,设计了一份测试卷,要求检测对象在45分钟内学习特定的材料,并解答相关问题(满分100分).已知被测试者的学习能力指标P与其所得分数x(分)和完成所需时间t(分钟)存在函数关系:p=ktx2+mx.在检测过程中得到如下数据:
(1)求k和m的值;
(2)小红用了35分钟完成了该项测试,其成绩为80分,试确定其学习能力指标P的值;
(3)小红用了25分钟完成了该项检测,要使小兵的学习能力指标P取最大值,他检测成绩应该是多少分?
| 检测成绩x(分) | 完成时间t(分钟) | 学习能力指标p | |
| 1 | 100 | 30 | 90 |
| 2 | 100 | 40 | 80 |
(2)小红用了35分钟完成了该项测试,其成绩为80分,试确定其学习能力指标P的值;
(3)小红用了25分钟完成了该项检测,要使小兵的学习能力指标P取最大值,他检测成绩应该是多少分?
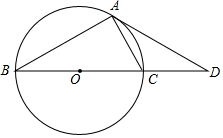 如图,已知BC是⊙O的直径,点D为BC延长线上的一点,点A为圆上一点,且AB=AD,AC=CD.
如图,已知BC是⊙O的直径,点D为BC延长线上的一点,点A为圆上一点,且AB=AD,AC=CD.