题目内容
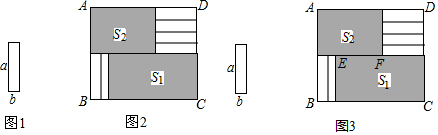
8.搭成1个三角形用3根火柴棒,接着用火柴棒按如图所示的方式搭成2个三角形,再用火柴棒搭成3个三角形、4个三角形…
(1)若这样的三角形有6个时,则需要火柴棒13根.
(2)若这样的三角形有n个时,则需要火柴棒2n+1根.(代数式需化简)
(3)若用了1001根火柴棒,则可组成500个这样的三角形.
分析 (1)根据观察,可发现规律这样的三角形有n个时,则需要火柴棒2n+1跟,根据规律,可得答案;
(2)根据观察,可发现规律这样的三角形有n个时,则需要火柴棒2n+1跟,根据规律,可得答案;
(3)根据观察,可发现规律这样的三角形有n个时,则需要火柴棒2n+1跟,根据规律,可得答案.
解答 解:观察:第一个是2+1,
第二个是2×2+1,
第三个是2×3+1,
(1)若这样的三角形有6个时,则需要火柴棒2×6+1=13根
(2)若这样的三角形有n个时,则需要火柴棒2n+1跟;
(3)设可组成n个三角形,由题意,得
2n+1=1001,
解得n=500,
故答案为:13,2n+1,500.
点评 本题考查了规律性,观察发现规律是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.使一次函数y=(m+2)x+m-2不经过第二象限,且使关于x的不等式组$\left\{\begin{array}{l}{x>m-2}\\{-3x+2≥6m-1}\end{array}\right.$有解的所有整数m的和为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
3.如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):

(1)填写下表:
(2)前5个正方形分割的三角形的和40前n个正方形分割的三角形的和n2+3n,
(3)原正方形能否被分割成2 012个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.

(1)填写下表:
| 正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
| 分割成的三角形的个数 | 4 | 6 | … |
(3)原正方形能否被分割成2 012个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.
13.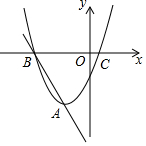 已知抛物线y1=x2+2x-3的顶点为A,与x轴交于点B、C(B在C的左边),直线y2=kx+b过A、B两点.
已知抛物线y1=x2+2x-3的顶点为A,与x轴交于点B、C(B在C的左边),直线y2=kx+b过A、B两点.
(1)求直线AB的解析式;
(2)当y1<y2时,根据图象直接写出自变量x的取值范围.
 已知抛物线y1=x2+2x-3的顶点为A,与x轴交于点B、C(B在C的左边),直线y2=kx+b过A、B两点.
已知抛物线y1=x2+2x-3的顶点为A,与x轴交于点B、C(B在C的左边),直线y2=kx+b过A、B两点.(1)求直线AB的解析式;
(2)当y1<y2时,根据图象直接写出自变量x的取值范围.
18.下列事件中,属于必然事件的是( )
| A. | 在只装了红球的袋子中摸到白球 | |
| B. | 某射击运动员射击一次,命中靶心 | |
| C. | 任意画一个三角形,其内角和是180° | |
| D. | 掷一枚质地均匀的正方体骰子,向上的一面点数是3 |