题目内容
17.一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件如图1,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.(1)求证:△AEF∽△ABC;
(2)求这个正方形零件的边长;

分析 (1)根据四边形EFHG是正方形,可得EF∥BC,所以△AEF∽△ABC.
(2)设这个正方形零件的边长是xmm,根据$\frac{EF}{BC}$=$\frac{AK}{AD}$,求出这个正方形零件的边长是多少即可.
解答 (1)证明:∵四边形EFHG是正方形,
∴EF∥BC,
∴△AEF∽△ABC.
(2)解:设这个正方形零件的边长是xmm,
∵EF∥BC,
∴$\frac{EF}{BC}$=$\frac{AK}{AD}$,
∴$\frac{x}{120}$=$\frac{80-x}{80}$,
解得x=48
答:这个正方形零件的边长是48mm.
点评 此题主要考查了正方形的特征和应用,以及三角形相似的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①三边法:三组对应边的比相等的两个三角形相似;②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;③两角法:有两组角对应相等的两个三角形相似.

练习册系列答案
相关题目
5.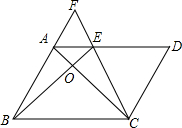 如图,点E是平行四边形ABCD边AD上一点,且AE=$\frac{1}{2}$ED,BA、CE的延长线交于点F,BE与AC交于点O,则下列结论:①相似三角形有2对,②AB=2AF,③8S△AOE=S△CED,④S四边形ABCE=2S△CED中正确的有( )
如图,点E是平行四边形ABCD边AD上一点,且AE=$\frac{1}{2}$ED,BA、CE的延长线交于点F,BE与AC交于点O,则下列结论:①相似三角形有2对,②AB=2AF,③8S△AOE=S△CED,④S四边形ABCE=2S△CED中正确的有( )
 如图,点E是平行四边形ABCD边AD上一点,且AE=$\frac{1}{2}$ED,BA、CE的延长线交于点F,BE与AC交于点O,则下列结论:①相似三角形有2对,②AB=2AF,③8S△AOE=S△CED,④S四边形ABCE=2S△CED中正确的有( )
如图,点E是平行四边形ABCD边AD上一点,且AE=$\frac{1}{2}$ED,BA、CE的延长线交于点F,BE与AC交于点O,则下列结论:①相似三角形有2对,②AB=2AF,③8S△AOE=S△CED,④S四边形ABCE=2S△CED中正确的有( )| A. | 3个 | B. | 2个 | C. | 4个 | D. | 1个 |
9.若1-$\frac{4}{x}$+$\frac{4}{{x}^{2}}$=9,则$\frac{2}{x}$的值是( )
| A. | 4 | B. | -2 | C. | 4或-2 | D. | ±3 |
7.袋中装有除颜色外完全相同的a个白球、b个红球、c个黄球,则任意摸出一个球是黄球的概率为( )
| A. | $\frac{c}{a+b+c}$ | B. | $\frac{c}{a+b}$ | C. | $\frac{a+c}{a+b+c}$ | D. | $\frac{a+b}{c}$ |
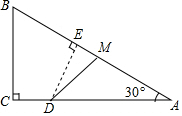 如图,Rt△ABC中,∠C=90°,∠A=30°,BC=6,点M在AB上,且AM=4,点D是AC边上的一个动点(不与A、C重合),设CD的长为x,△ADM的面积y
如图,Rt△ABC中,∠C=90°,∠A=30°,BC=6,点M在AB上,且AM=4,点D是AC边上的一个动点(不与A、C重合),设CD的长为x,△ADM的面积y
 如图,在等边△ABC中,AB=8cm,AD⊥BC,DE⊥AB,DF⊥AC,垂足分别是D,E,F,则BE=2cm.
如图,在等边△ABC中,AB=8cm,AD⊥BC,DE⊥AB,DF⊥AC,垂足分别是D,E,F,则BE=2cm.