题目内容
16.使一次函数y=(m+2)x+m-2不经过第二象限,且使关于x的不等式组$\left\{\begin{array}{l}{x>m-2}\\{-3x+2≥6m-1}\end{array}\right.$有解的所有整数m的和为( )| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
分析 根据一次函数图象与系数的关系可得出关m的一元一次不等式组,解之即可得出m的取值范围,再由关于x的不等式组有解可得出m的取值范围,结合m为整数即可得出m的值,进而即可得出结论.
解答 解:∵一次函数y=(m+2)x+m-2不经过第二象限,
∴$\left\{\begin{array}{l}{m+2>0}\\{m-2≤0}\end{array}\right.$,
∴-2<m≤2.
∵关于x的不等式组$\left\{\begin{array}{l}{x>m-2}\\{-3x+2≥6m-1}\end{array}\right.$有解,
∴m<1.
∵m为整数,
∴m的值为:-1,0.
故选A.
点评 本题考查了一次函数图象与系数的关系以及一次函数与一元一次不等式,通过解不等式组以及不等式有解找出m值是解题的关键.

练习册系列答案
相关题目
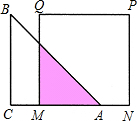 如图,等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时A点与M点重合,让向右运动,最后A点与N点重合,则重叠部分面积ycm2与MA长度xcm之间关系式y=$\frac{1}{2}$x2;自变量的取值范围是0<x≤10.
如图,等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时A点与M点重合,让向右运动,最后A点与N点重合,则重叠部分面积ycm2与MA长度xcm之间关系式y=$\frac{1}{2}$x2;自变量的取值范围是0<x≤10.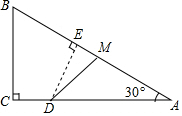 如图,Rt△ABC中,∠C=90°,∠A=30°,BC=6,点M在AB上,且AM=4,点D是AC边上的一个动点(不与A、C重合),设CD的长为x,△ADM的面积y
如图,Rt△ABC中,∠C=90°,∠A=30°,BC=6,点M在AB上,且AM=4,点D是AC边上的一个动点(不与A、C重合),设CD的长为x,△ADM的面积y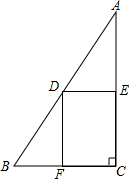 如图,在Rt△ABC中,∠C=90°,BC=6,AC=12,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为点E,F,得四边形DECF,设DE=x,DF=y.
如图,在Rt△ABC中,∠C=90°,BC=6,AC=12,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为点E,F,得四边形DECF,设DE=x,DF=y. 如图所示,D是BC的中点,E是AC的中点,若S△ADE=1,则S△ABC=4.
如图所示,D是BC的中点,E是AC的中点,若S△ADE=1,则S△ABC=4.
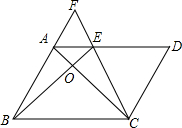 如图,点E是平行四边形ABCD边AD上一点,且AE=$\frac{1}{2}$ED,BA、CE的延长线交于点F,BE与AC交于点O,则下列结论:①相似三角形有2对,②AB=2AF,③8S△AOE=S△CED,④S四边形ABCE=2S△CED中正确的有( )
如图,点E是平行四边形ABCD边AD上一点,且AE=$\frac{1}{2}$ED,BA、CE的延长线交于点F,BE与AC交于点O,则下列结论:①相似三角形有2对,②AB=2AF,③8S△AOE=S△CED,④S四边形ABCE=2S△CED中正确的有( )