题目内容
19.将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,求a,b满足的关系式.(1)为解决上述问题,如图3,小明设EF=x,则可以表示出S1=a(x+a),S2=4b(x+2b);
(2)求a,b满足的关系式,写出推导过程.
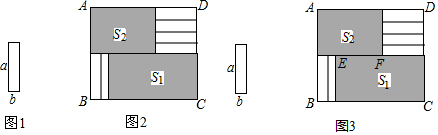
分析 (1)根据题意得出面积即可;
(2)表示出左上角与右下角部分的面积,求出它们的差,根据它们的差与BC无关即可求出a与b的关系式.
解答 解:(1)S1=a(x+a),S2=4b(x+2b),故答案为:a(x+a),4b(x+2b),
(2)由(1)知:
S1=a(x+a),S2=4b(x+2b),
∴S1-S2
=a(x+a)-4b(x+2b)
=ax+a2-4bx-8b2
=(a-4b)x+a2-8b2,
∵S1与S2的差总保持不变,
∴a-4b=0.
∴a=4b.
点评 此题考查了整式的混合运算的应用,弄清题意是解本题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
9.若1-$\frac{4}{x}$+$\frac{4}{{x}^{2}}$=9,则$\frac{2}{x}$的值是( )
| A. | 4 | B. | -2 | C. | 4或-2 | D. | ±3 |
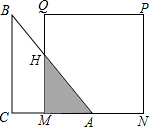 如图,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为20cm,AC与MN在同一条直线上,开始时点A与点N重合,让△ABC以2cm/s的速度向左运动,最终点A与点M重合.求:
如图,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为20cm,AC与MN在同一条直线上,开始时点A与点N重合,让△ABC以2cm/s的速度向左运动,最终点A与点M重合.求: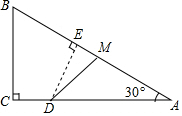 如图,Rt△ABC中,∠C=90°,∠A=30°,BC=6,点M在AB上,且AM=4,点D是AC边上的一个动点(不与A、C重合),设CD的长为x,△ADM的面积y
如图,Rt△ABC中,∠C=90°,∠A=30°,BC=6,点M在AB上,且AM=4,点D是AC边上的一个动点(不与A、C重合),设CD的长为x,△ADM的面积y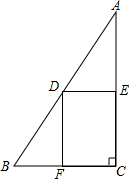 如图,在Rt△ABC中,∠C=90°,BC=6,AC=12,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为点E,F,得四边形DECF,设DE=x,DF=y.
如图,在Rt△ABC中,∠C=90°,BC=6,AC=12,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为点E,F,得四边形DECF,设DE=x,DF=y.