题目内容
3.如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
(1)填写下表:
| 正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
| 分割成的三角形的个数 | 4 | 6 | … |
(3)原正方形能否被分割成2 012个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.
分析 (1)根据图形特点找出正方形ABCD内点的个数与分割成的三角形的个数的关系,总结规律即可;
(2)将(1)中的规律写出来即可;
(2)根据规律列出方程,解方程得到答案.
解答 解:(1)有1个点时,内部分割成4个三角形;
有2个点时,内部分割成4+2=6个三角形;
有3个点时,内部分割成4+2×2=8个三角形;
有4个点时,内部分割成4+2×3=10个三角形; …
以此类推,有n个点时,内部分割成4+2×(n-1)=(2n+2)个三角形;
(2)前5个正方形分割的三角形的和40,前n个正方形分割的三角形的和为n2+3n,
(3)能.理由如下:由(1)知2n+2=2012,解得n=1005,
∴此时正方形ABCD内部有1005点.
点评 本题考查的是图形的变化类问题,正确理解题意、根据图形的特点正确找出规律是解题的关键.

练习册系列答案
相关题目
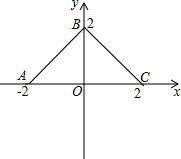 如图,在直角坐标系上有折线段ABC,它们的坐标分别是A(-2,0),B(0,2),C(2,0),若有动直线l:y=t(0<t<2)线段AB交于M,与线段BC交于N,如果记三角形MNO的面积为S.
如图,在直角坐标系上有折线段ABC,它们的坐标分别是A(-2,0),B(0,2),C(2,0),若有动直线l:y=t(0<t<2)线段AB交于M,与线段BC交于N,如果记三角形MNO的面积为S. 如图,已知∠ABC=∠ADC,BE,DF分别平分∠ABC,∠ADC,且∠1=∠2,请说明:∠A=∠C.
如图,已知∠ABC=∠ADC,BE,DF分别平分∠ABC,∠ADC,且∠1=∠2,请说明:∠A=∠C.
 如图,在等边△ABC中,AB=8cm,AD⊥BC,DE⊥AB,DF⊥AC,垂足分别是D,E,F,则BE=2cm.
如图,在等边△ABC中,AB=8cm,AD⊥BC,DE⊥AB,DF⊥AC,垂足分别是D,E,F,则BE=2cm.