题目内容
4.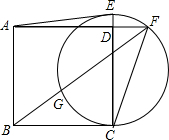 如图,已知正方形ABCD的边长为2,在CD的延长线上取一点E,以CE为直径作圆交AD的延长线于点F,连接FB交圆于另一点G,且GB=DF.
如图,已知正方形ABCD的边长为2,在CD的延长线上取一点E,以CE为直径作圆交AD的延长线于点F,连接FB交圆于另一点G,且GB=DF.(1)证明:GF=CE.
(2)试求五边形ABCFE的面积.
分析 (1)只要证明△AGH∽△AFG即可解决问题.
(2)设BG=DF=DH=x,圆的半径为R,则BF=x+2R,AF=2+x,DE=2R-2,由勾股定理和相交弦定理得到,推出2R+xR=4,再根据S五边形ABCFE=S正方形ABCD+S△ADE+S△ECF=2+2R+xR即可解决问题.
解答 (1)证明:连接AG,GH,
∵正方形ABCD,
∴∠BCD=∠ADC=90°,AB=BC,
∵CE为圆的直径,
∴BC是圆的切线,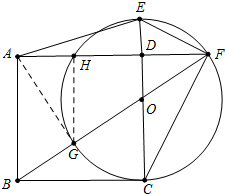
∴BC2=BG•BF,
∴AB2=BG•BF,
∴$\frac{AB}{BF}=\frac{BG}{AB}$,
∵∠ABG=∠FBA,
∴△ABG∽△FBA,
∴∠AGB=∠BAF=90°,
∴AG2=AB2-BG2=AD2-DF2=(AD+DF)(AD-DF)=AF(AD-AF),
∵CE为圆的直径,∠ADC=90°,
∴DF=DH,
∴AG2=AF•AH,
∴$\frac{AG}{AF}=\frac{AH}{AG}$,
∵∠FAG=∠GAH,
∴△AGH∽△AFG,
∴∠AHG=∠AGF=90°,
∴FG是圆的直径,
∴FG=CE;
(2)解:设BG=DF=DH=x,圆的半径为R,则BF=x+2R,AF=2+x,DE=2R-2,由勾股定理和相交弦定理得到,
BO2=CB2+CO2,CD•DE=DF•DH,
∴(x+R)2=R2+22,2(2R-2)=x2,
∴x2+2xR=4,4R-4=x2,
∴4R-4+2xR=4,
∴4R+2xR=8,
∴2R+xR=4,
∴S五边形ABCFE=S正方形ABCD+S△ADE+S△ECF=2+2R+xR=2+4=6.
点评 本题考查圆综合题、相似三角形的判定和性质、勾股定理等知识,解题的关键是灵活应用这些知识解决问题,学会添加辅助线,构造相似三角形,学会利用参数解决问题,注意整体思想在本题中的体现,属于中考压轴题.

| A. | -2 | B. | 3 | C. | 4 | D. | -4 |
| A. | x≥1 | B. | 0<x≤1 | C. | x>0 | D. | 0≤x≤1 |
| A. | -$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $-\sqrt{3}+2$ | D. | $\sqrt{3}$+2 |
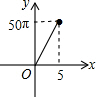
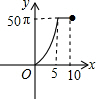
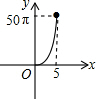
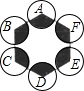 如图,正六边形的边长为10,分别以正六边形的顶点A、B、C、D、E、F为圆心,画6个全等的圆.若圆的半径为x,且0<x≤5,阴影部分的面积为y,能反映y与x之间函数关系的大致图形是( )
如图,正六边形的边长为10,分别以正六边形的顶点A、B、C、D、E、F为圆心,画6个全等的圆.若圆的半径为x,且0<x≤5,阴影部分的面积为y,能反映y与x之间函数关系的大致图形是( )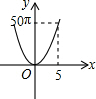
 如图,一只蚂蚁在某公园的位置平面图上爬行,它从西门出发,沿北偏东60°的方向爬行400cm到达望春亭,在望春亭停留片刻,小蚂蚁又沿北偏西60°的方向爬行400cm到达中心广场.
如图,一只蚂蚁在某公园的位置平面图上爬行,它从西门出发,沿北偏东60°的方向爬行400cm到达望春亭,在望春亭停留片刻,小蚂蚁又沿北偏西60°的方向爬行400cm到达中心广场.