题目内容
1.己知,不等式组$\left\{\begin{array}{l}{x+9<5x+1}\\{x>m+1}\end{array}\right.$的解集是x>2.(1)求m的取值范围;
(2)若$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$是方程2x-3=ay的一组解,化简:|a-m|-|m-2a|.
分析 (1)原不等式组变形后由其解集根据“同大取大”可得m的范围;
(2)将x、y的值代入后求得a的值,根据绝对值性质化简原式.
解答 解:(1)原不等式组变形为$\left\{\begin{array}{l}{x>2}\\{x>m+1}\end{array}\right.$,
∵不等式组的解集为x>2,
∴m+1≤2,即m≤1;
(2)∵$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$是方程2x-3=ay的一组解,
∴2-3=-a,解得:a=1,
∴原式=|1-m|-|m-2|
=1-m-(2-m)
=1-m-2+m
=-1.
点评 本题主要考查一元一次不等式组的解集和方程的解及绝对值性质,熟练掌握不等式组解集的确定原则和方程的解得概念、绝对值性质是关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
9.下列图案中既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
16.若二项式4a2+ma+1是一个含a的完全平方式,则m等于( )
| A. | 4 | B. | 4或-4 | C. | 2 | D. | 2或-2 |
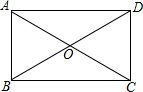 如图,矩形ABCD的对角线AC,BD相交于点O,点E,F,M,N分别为OA,OB,OC,OD的中点,连接EF,FM,MN,NE.
如图,矩形ABCD的对角线AC,BD相交于点O,点E,F,M,N分别为OA,OB,OC,OD的中点,连接EF,FM,MN,NE.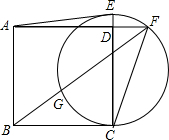 如图,已知正方形ABCD的边长为2,在CD的延长线上取一点E,以CE为直径作圆交AD的延长线于点F,连接FB交圆于另一点G,且GB=DF.
如图,已知正方形ABCD的边长为2,在CD的延长线上取一点E,以CE为直径作圆交AD的延长线于点F,连接FB交圆于另一点G,且GB=DF.