题目内容
9.规定x=x0时,代数式$\frac{x^2}{{1+{x^2}}}$的值记为f(x0).例如:x=-1时,$f(-1)=\frac{{{{(-1)}^2}}}{{1+{{(-1)}^2}}}=\frac{1}{2}$,则$f(1)+f(2)+f(3)+…+f(168)+f(\frac{1}{2})+f(\frac{1}{3})+f(\frac{1}{4})+…+f(\frac{1}{168})$的值等于167$\frac{1}{2}$.分析 根据题意得到f(x)+f($\frac{1}{x}$)=1,原式结合后,计算即可得到结果.
解答 解:根据题意得:f(x)+f($\frac{1}{x}$)=$\frac{{x}^{2}}{1+{x}^{2}}$+$\frac{\frac{1}{{x}^{2}}}{1+\frac{1}{{x}^{2}}}$=$\frac{{x}^{2}}{1+{x}^{2}}$+$\frac{1}{{x}^{2}+1}$=$\frac{{x}^{2}+1}{{x}^{2}+1}$=1,
则原式=f(1)+[f(2)+f($\frac{1}{2}$)]+[f(3)+f($\frac{1}{3}$)]+[f(4)+f($\frac{1}{4}$)]+…[f(168)+f($\frac{1}{168}$)]=$\frac{1}{2}$+167=167$\frac{1}{2}$,
故答案为:167$\frac{1}{2}$
点评 此题考查了分式的值,根据题意得到f(x)+f($\frac{1}{x}$)=1是解本题的关键.

练习册系列答案
相关题目
5.下列图案是轴对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.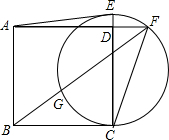 如图,已知正方形ABCD的边长为2,在CD的延长线上取一点E,以CE为直径作圆交AD的延长线于点F,连接FB交圆于另一点G,且GB=DF.
如图,已知正方形ABCD的边长为2,在CD的延长线上取一点E,以CE为直径作圆交AD的延长线于点F,连接FB交圆于另一点G,且GB=DF.
(1)证明:GF=CE.
(2)试求五边形ABCFE的面积.
 如图,已知正方形ABCD的边长为2,在CD的延长线上取一点E,以CE为直径作圆交AD的延长线于点F,连接FB交圆于另一点G,且GB=DF.
如图,已知正方形ABCD的边长为2,在CD的延长线上取一点E,以CE为直径作圆交AD的延长线于点F,连接FB交圆于另一点G,且GB=DF.(1)证明:GF=CE.
(2)试求五边形ABCFE的面积.
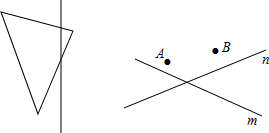 (1)以直线为对称轴,画出下列图形的另一部分使它们成为轴对称图形.
(1)以直线为对称轴,画出下列图形的另一部分使它们成为轴对称图形.