题目内容
16.已知$a=\frac{\sqrt{3}-1}{2}$,则$\frac{2{a}^{3}+6{a}^{2}+a}{2{a}^{2}-1}$=( )| A. | -$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $-\sqrt{3}+2$ | D. | $\sqrt{3}$+2 |
分析 由条件可求得2a+$\frac{1}{a}$及2a-$\frac{1}{a}$,再把所求的式子化为与之相关的代数式,代入计算求值即可.
解答 解:
∵$a=\frac{\sqrt{3}-1}{2}$,
∴$\frac{1}{a}$=$\frac{2}{\sqrt{3}-1}$=$\frac{2(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}$=$\frac{2(\sqrt{3}+1)}{2}$=$\sqrt{3}$+1,
∴2a+$\frac{1}{a}$=$\sqrt{3}$-1+$\sqrt{3}$+1=2$\sqrt{3}$,2a-$\frac{1}{a}$=$\sqrt{3}$-1-($\sqrt{3}$+1)=-2,
∴$\frac{2{a}^{3}+6{a}^{2}+a}{2{a}^{2}-1}$
=$\frac{a(2{a}^{2}+6a+1)}{2{a}^{2}-1}$
=$\frac{2{a}^{2}+6a+1}{2a-\frac{1}{a}}$
=$\frac{2{a}^{2}+6a+1}{-2}$
=$\frac{a(2a+6+\frac{1}{a})}{-2}$
=$\frac{a(2\sqrt{3}+6)}{-2}$
=$\frac{2a(\sqrt{3}+3)}{-2}$
=-a$\sqrt{3}$(1+$\sqrt{3}$)
=-$\sqrt{3}$×$\frac{\sqrt{3}-1}{2}$×(1+$\sqrt{3}$)
=-$\sqrt{3}$,
故选A.
点评 本题主要考查二次根式的化简,熟练掌握二次根式的运算性质及乘法公式是解题的关键,巧妙利用2a和$\frac{1}{a}$的关系可以起到简化运算的作用.

练习册系列答案
相关题目
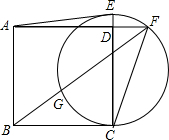 如图,已知正方形ABCD的边长为2,在CD的延长线上取一点E,以CE为直径作圆交AD的延长线于点F,连接FB交圆于另一点G,且GB=DF.
如图,已知正方形ABCD的边长为2,在CD的延长线上取一点E,以CE为直径作圆交AD的延长线于点F,连接FB交圆于另一点G,且GB=DF. (1)以直线为对称轴,画出下列图形的另一部分使它们成为轴对称图形.
(1)以直线为对称轴,画出下列图形的另一部分使它们成为轴对称图形.