题目内容

15．如图：
（1）已知∠2=∠3，则AD∥BC．
（2）已知∠1=∠4，则AB∥DC．

分析 （1）因为∠2=∠3，在图中发现AD、BC被BD所截，故可按内错角相等两直线平行进行判定．
（2）因为∠1=∠4，在图中发现AB、DC被BD所截，故可按内错角相等两直线平行进行判定．

解答 解：（1）∵∠2=∠3，
∴AD∥BC（内错角相等两直线平行）．
（2）∵∠1=∠4，
∴AB∥DC（内错角相等两直线平行）．
故答案为：AD；BC；AB；DC．

点评 此题考查平行线的判定，解答此类要判定两直线平行的题，可围绕截线找同位角、内错角和同旁内角．本题能有效地培养“执果索图”的思维方式与能力．

练习册系列答案
相关题目
5．如果一个扇形所含圆弧的长是相同半径圆周长的$\frac{1}{5}$，那么这个扇形的面积是这个圆面积的$\frac{1}{5}$．
6．如图，线段AB表示一根对折以后的绳子，现从P处把绳子剪断，剪断后的各段绳子中最长的一段8cm，若AP=$\frac{1}{2}$PB，则这条绳子的原长为（　　）cm．
A．12B．24C．20 或24D．12或24
3．已知abc＞0，ab＜0，则$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=-1．
10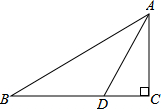．如图，在△ABC中，∠C=90°，AC=2，点D在BC上，∠ADC=2∠B，AD=$\sqrt{5}$，则BC的长为（　　）
A．$\sqrt{3}$-1B．$\sqrt{3}$+1C．$\sqrt{5}$+1D．$\sqrt{5}$-1
20．已知实数p、q、r满足p+q+r=26，$\frac{1}{p}$+$\frac{1}{q}$+$\frac{1}{r}$=31，则$\frac{p}{q}$+$\frac{q}{r}$+$\frac{r}{p}$+$\frac{p}{r}$+$\frac{r}{q}$+$\frac{q}{p}$=803．
7．判断命题“互补的角是同旁内角”是真命题还是假命题，如果是真命题，说出它的题设和结论；如果是假命题，请举出一个反例．（要求：画出相应的图形，并用文字语言或符号语言表述所举反例）．
4．△ABC中，∠C=90°，D是AC边上一点，且CD=CB，AD=BD，则tanA的值是（　　）
A．$\sqrt{2}$B．$\sqrt{2}$-1C．$\frac{\sqrt{2}}{2}$D．不能确定
5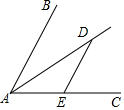．如图，∠BAC=60°，AD是∠BAC的角平分线，点D在AD上，过点D作DE∥AB交AC于点E．若DE=2，则点D到AB的距离为（　　）
A．1B．$\sqrt{3}$C．2D．2$\sqrt{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网