题目内容
5.如果一个扇形所含圆弧的长是相同半径圆周长的$\frac{1}{5}$,那么这个扇形的面积是这个圆面积的$\frac{1}{5}$.分析 根据题干分析可得,扇形所对的弧长是等圆的周长的$\frac{1}{5}$,则这个扇形的圆心角的度数就是这个圆的圆心角的$\frac{1}{5}$,由此根据扇形的面积公式即可得出,这个扇形的面积是这个圆的面积的$\frac{1}{5}$.
解答 解:1°圆心角所对的弧长=$\frac{2πr}{360}$,若扇形所对的弧长是等圆的周长的$\frac{1}{5}$,则这条弧长所对的圆心角是72°,
$\frac{72°}{360°}$=$\frac{1}{5}$,因为扇形的面积=$\frac{圆心角的度数}{360}$×πr2,
所以这个扇形的面积是:$\frac{72}{360}$×πr2=$\frac{1}{5}$πr2,
所以这个扇形的面积就是这个圆的面积的$\frac{1}{5}$.
故答案为:$\frac{1}{5}$.
点评 解答此题的关键是灵活应用弧长公式求出这个扇形的圆心角的度数,再利用扇形的面积公式即可得出这个扇形占整个圆的面积的几分之几.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列运算正确的是( )
| A. | $\sqrt{4}$=±2 | B. | (-3)3=27 | C. | $\sqrt{16}$=4 | D. | $\root{3}{9}$=3 |
3. 如图是由射线AB,BC,CD,DE,EA组成的平面图形,若∠1+∠2+∠3+∠4=225°,ED∥AB,则∠1的度数为( )
如图是由射线AB,BC,CD,DE,EA组成的平面图形,若∠1+∠2+∠3+∠4=225°,ED∥AB,则∠1的度数为( )
 如图是由射线AB,BC,CD,DE,EA组成的平面图形,若∠1+∠2+∠3+∠4=225°,ED∥AB,则∠1的度数为( )
如图是由射线AB,BC,CD,DE,EA组成的平面图形,若∠1+∠2+∠3+∠4=225°,ED∥AB,则∠1的度数为( )| A. | 55° | B. | 45° | C. | 35° | D. | 25° |
 如图,在等边△ABC中,点D为边BC的中点,以AD为边作等边△ADE,连接BE.
如图,在等边△ABC中,点D为边BC的中点,以AD为边作等边△ADE,连接BE.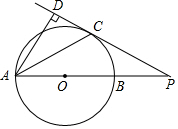 如图,AB是⊙O的直径,PC切⊙O于点C,AB的延长线与PC交于点P,PC的延长线与AD交于点D,AC平分∠DAB.
如图,AB是⊙O的直径,PC切⊙O于点C,AB的延长线与PC交于点P,PC的延长线与AD交于点D,AC平分∠DAB. 如图:
如图: