题目内容
10．一个十位数字为零的三位数，它恰好等于其各位数字和的m倍，交换它的个位数字与百位数字后所得到的新数又是其各位数字和的n倍，则m+n的值是（ ）| A． | 99 | B． | 100 | C． | 101 | D． | 110 |
分析 设个位数字为x，百位数为y，根据题中描述可得到两个等量关系，求解即可．
解答 解：设个位数字为x，百位数为y，根据题意得：
$\left\{\begin{array}{l}{100y+x=（x+y）m}\\{100x+y=（x+y）n}\end{array}\right.$，
两方程相加，得101x+101y=（x+y）（m+n），
解得m+n=101．
故选C．
点评 本题考查了二元一次方程组的应用及解法，解题关键是弄清题意，合适的等量关系，列出方程组．
本题涉及一个常识问题：三位数=100×百位数字+10×十位数字+个位数字，并且在求两位数或三位数时，一般是不能直接设这个两位数或三位数的，而是设它各个数位上的数字为未知数．注意当方程组中的未知数较多时要观察运用整体消元来解未知数．
练习册系列答案
阶梯计算系列答案
相关题目
20．
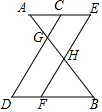如图，AE∥BD，点C，F分别在线段AE，BD上，连接CD，FE，分别与AB相交于点G、H，若CD∥EF，则下列结论一定正确的是（ ）
如图，AE∥BD，点C，F分别在线段AE，BD上，连接CD，FE，分别与AB相交于点G、H，若CD∥EF，则下列结论一定正确的是（ ）| A． | $\frac{CG}{CD}$=$\frac{EH}{HF}$ | B． | $\frac{AG}{GB}$=$\frac{AC}{CD}$ | C． | $\frac{CE}{GH}$=$\frac{DF}{BG}$ | D． | $\frac{GC}{HE}$=$\frac{AC}{AE}$ |
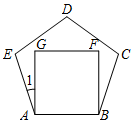有一个正五边形和一个正方形边长相等，如图放置，则∠1=18°．
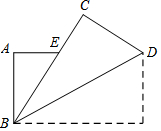如图，把长方形纸片ABCD纸沿对角线折叠，设重叠部分为△EBD，那么，有下列说法：
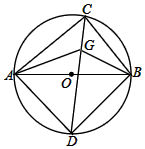如图，AB为⊙O的直径，C为上半圆上一点，D为下半圆弧的中点，G为CD上一点，满足DA=DG