题目内容
20.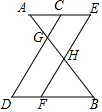 如图,AE∥BD,点C,F分别在线段AE,BD上,连接CD,FE,分别与AB相交于点G、H,若CD∥EF,则下列结论一定正确的是( )
如图,AE∥BD,点C,F分别在线段AE,BD上,连接CD,FE,分别与AB相交于点G、H,若CD∥EF,则下列结论一定正确的是( )| A. | $\frac{CG}{CD}$=$\frac{EH}{HF}$ | B. | $\frac{AG}{GB}$=$\frac{AC}{CD}$ | C. | $\frac{CE}{GH}$=$\frac{DF}{BG}$ | D. | $\frac{GC}{HE}$=$\frac{AC}{AE}$ |
分析 由于AE∥BD,CD∥EF,所以△ACG∽△GDB,△ACG∽△AEH,根据相似三角形的性质即可判断.
解答 解:∵AE∥BD,
∴△ACG∽△BDG,
∴$\frac{AC}{BD}$=$\frac{AG}{BG}$
∵CD∥EF,
∴△ACG∽△AEH,
∴$\frac{AC}{AE}=\frac{CG}{HE}$
故选(D)
点评 本题考查相似三角形的判定,解题的关键是利用AE∥BD,CD∥EF,证明△ACG∽△GDB,△ACG∽△AEH,本题属于基础题型.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
10.下列说法中错误的是( )
| A. | 三角形的中线、角平分线,高线都是线段 | |
| B. | 有一个内角是直角的三角形是直角三角形 | |
| C. | 任意三角形的外角和都是360° | |
| D. | 三角形的一个外角大于任何一个内角 |
11.已知方程x2+4x+4=0,则该方程的根的情况为( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 没有实数根 | D. | 无法判断 |
10.一个十位数字为零的三位数,它恰好等于其各位数字和的m倍,交换它的个位数字与百位数字后所得到的新数又是其各位数字和的n倍,则m+n的值是( )
| A. | 99 | B. | 100 | C. | 101 | D. | 110 |