Question

8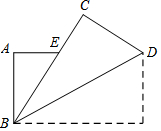．如图，把长方形纸片ABCD纸沿对角线折叠，设重叠部分为△EBD，那么，有下列说法：
①△EBD是等腰三角形，EB=ED；
②折叠后∠ABE和∠CBD和一定相等；
③折叠后得到的图形是轴对称图形；
④若AB=4，AD=8，则AE=3．
其中正确的是①③④．（请写上正确的序号）

Answer 1

分析 根据轴对称的性质可以得出DC=DC′，BC′=BC，∠DBC=∠DBC′，再由矩形的性质就可以得出∠EBD=∠EDB，就可以得出BE=DE，得出△EBD是等腰三角形，进而可以由AAS证明△EBA≌△EDC，可得BE=DE，根据勾股定理可求AE，就可以得出折叠后的图形关于BD的中垂线对称，从而得出结论．

解答 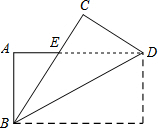解：如图，∵四边形ABCD是矩形，
∴AB=CD，AD=BC，∠A=C=90°，AD∥BC，
∴∠ADB=∠CBD．
∵△DBC与△DBC′关于BD对称，
∴△DBC≌△DBC′，
∴DC=DC′，BC′=BC，∠DBC=∠DBC′，∠C=∠C′．
∴AB=C′D，∠A=∠C′．∠EBD=∠EDB，
∴BE=DE，
∴△EBD是等腰三角形．故①正确．
在△AEB和△C′ED中，
$\left\{\begin{array}{l}{∠A=∠C′}\\{∠AEB=∠C′ED}\\{AB=C′D}\end{array}\right.$，
∴△AEB≌△C′ED（AAS），
∴BE=DE，
在Rt△BAE中，AE²+AB²=BE²，即AE²+4²=（8-AE）²，
解得AE=3，．故④正确，
∴折叠后得到的图形是轴对称图形，故③正确．
∵∠DBC=∠DBC′，
∴∠ABE和∠CBD不一定相等．故②错误．
故答案为：①③④．

点评 此题考查了矩形的性质的运用，轴对称的性质的运用，等腰三角形的判定及性质的运用，全等三角形的判定与性质的运用，勾股定理的运用，解答时运用轴对称的性质求解是关键．