题目内容
2.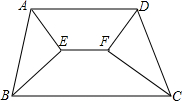 如图,梯形ABCD中,AD∥BC,∠BAD和∠ABC的平分线相交于点E,∠BCD和∠CDA的平分线相交于点F,求证:EF∥BC∥AD.
如图,梯形ABCD中,AD∥BC,∠BAD和∠ABC的平分线相交于点E,∠BCD和∠CDA的平分线相交于点F,求证:EF∥BC∥AD.
分析 分别延长AE、DF交BC于点G、H,利用角平分线的性质,平行线的性质求得E、F分别是AG、DH的中点,进一步利用平行线分线段成比例得出结论即可.
解答 解:如图,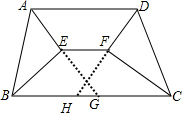
延长AE、DF交BC于点G、H,
∵AD∥BC,
∴∠BAD+∠ABC=180°,
∵AE、BE是∠BAD和∠ABC的平分线,
∴∠BAE+∠ABE=$\frac{1}{2}$(∠BAD+∠ABC)=90°,
∴∠AEB=90°,
又∵∠ABE=∠CBE,
∴AE=EG,
同理由AD∥BC,∠BCD和∠CDA的平分线相交于点F,
证得DF=FH,
∴EF∥BC∥AD.
点评 此题考查梯形的性质,角平分线的性质,平行线的性质,三线合一,以及平行线分线段成比例,作出辅助线是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.若$\sqrt{\frac{x-2}{3-x}}$=$\frac{\sqrt{x-2}}{\sqrt{3-x}}$成立,则x的取值范围为( )
| A. | x≥2 | B. | x≤3 | C. | 2≤x≤3 | D. | 2≤x<3 |
7.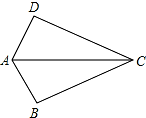 如图,已知DC=BC,那么添加下列一个条件后,就能判定△ABC≌△ADC的是( )
如图,已知DC=BC,那么添加下列一个条件后,就能判定△ABC≌△ADC的是( )
 如图,已知DC=BC,那么添加下列一个条件后,就能判定△ABC≌△ADC的是( )
如图,已知DC=BC,那么添加下列一个条件后,就能判定△ABC≌△ADC的是( )| A. | AD=AB | B. | ∠BAC=∠DAC | C. | BC=AC | D. | ∠B=∠D=90° |
 如图,AB∥CD,∠A=60°,∠C=25°,GH∥AE,则∠1=145°.
如图,AB∥CD,∠A=60°,∠C=25°,GH∥AE,则∠1=145°. ,小丽、小亮回忆说:
,小丽、小亮回忆说: