题目内容
14.已知a,b,c都是有理数,且满足$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=1.试判断a、b、c三个数中正数有几个.分析 根据有理数的除法:同号得正,异号得负,绝对值相除,可得答案.
解答 解:当a>0,b>0,c>0时,$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=3,
当a>0,b>0,c<0时,得$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=1,
当a>0,b<0,c<0时,$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=-1,
当a>0,b<0,c>0时,$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=1
当a<0,b<0,c<0时,$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=-3,
当a<0,b>0,c>0时,$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=1,
当a<0,b>0,c<0时,$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=-1,
当a<0,b<0,c>0时$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=-1
综上所述:a、b、c三个数中正数有2个时,$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=1.
点评 本题考查了有理数的除法,同号得正,异号得负,绝对值相除.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
4. 如图,DE∥AB,DF∥AC,∠A=60°,则∠FDE=( )
如图,DE∥AB,DF∥AC,∠A=60°,则∠FDE=( )
 如图,DE∥AB,DF∥AC,∠A=60°,则∠FDE=( )
如图,DE∥AB,DF∥AC,∠A=60°,则∠FDE=( )| A. | 35° | B. | 55° | C. | 60° | D. | 70° |
5. 如图所示,AB∥CD∥EF,则图中相似三角形有( )
如图所示,AB∥CD∥EF,则图中相似三角形有( )
 如图所示,AB∥CD∥EF,则图中相似三角形有( )
如图所示,AB∥CD∥EF,则图中相似三角形有( )| A. | 4对 | B. | 3对 | C. | 2对 | D. | 1对 |
4.若有理数a,b满足a•b=1,则下列说法正确的是( )
| A. | a=b | B. | |a|=|b| | C. | a,b互为相反数 | D. | a,b互为倒数 |
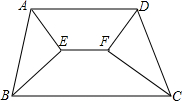 如图,梯形ABCD中,AD∥BC,∠BAD和∠ABC的平分线相交于点E,∠BCD和∠CDA的平分线相交于点F,求证:EF∥BC∥AD.
如图,梯形ABCD中,AD∥BC,∠BAD和∠ABC的平分线相交于点E,∠BCD和∠CDA的平分线相交于点F,求证:EF∥BC∥AD.