题目内容
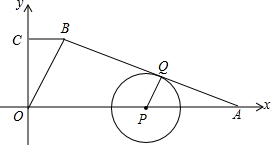 如图,在平面直角坐标系中,已知直角梯形OABC,BC∥OA,A(21,0),C(0,8),OB=10,点P在线段AO上运动,以点P为圆心作⊙P,使⊙P始终与AB边相切,切点为Q,设⊙P的半径为8x,
如图,在平面直角坐标系中,已知直角梯形OABC,BC∥OA,A(21,0),C(0,8),OB=10,点P在线段AO上运动,以点P为圆心作⊙P,使⊙P始终与AB边相切,切点为Q,设⊙P的半径为8x,(1)求点S△OAB的面积及AB;
(2)用x的代数式表示AP,并求出x的取值范围;
(3)请分别求出满足下列三个要求的x的值(写出简单的计算过程)
①点O在⊙P上;
②若⊙O的半径为16;⊙P与⊙O相切;
③⊙P与AB、OB都相切.
考点:圆的综合题,勾股定理,矩形的判定与性质,切线的性质,相切两圆的性质,相似三角形的判定与性质
专题:综合题
分析:(1)过点B作BH⊥OA于H,如图1,根据勾股定理可求出BC长,易证四边形BCOH是矩形,从而可求出BH、OH、AH的长,就可解决问题.
(2)过点B作BH⊥OA于H,过点B作BS⊥AB交OA于S,如图2,易证△PQA∽△BHA,根据相似三角形的性质就可用x的代数式表示AP长,由于⊙P始终与AB边相切,只需求出点B是切点时AP所对应的最大值AS,就可求出x的取值范围.
(3)①由条件可得OP=8x=21-17x,解这个方程就可得到对应的x的值;②可分⊙P与⊙O相外切和内切两种情况进行讨论,就可求出对应的x的值;③设⊙P与AB、OB分别相切于点F、E,连接PF、PE、BP,如图3.依据S△OAB=S△ABP+S△OBP建立关于x的方程,就可求出对应的x的值.
(2)过点B作BH⊥OA于H,过点B作BS⊥AB交OA于S,如图2,易证△PQA∽△BHA,根据相似三角形的性质就可用x的代数式表示AP长,由于⊙P始终与AB边相切,只需求出点B是切点时AP所对应的最大值AS,就可求出x的取值范围.
(3)①由条件可得OP=8x=21-17x,解这个方程就可得到对应的x的值;②可分⊙P与⊙O相外切和内切两种情况进行讨论,就可求出对应的x的值;③设⊙P与AB、OB分别相切于点F、E,连接PF、PE、BP,如图3.依据S△OAB=S△ABP+S△OBP建立关于x的方程,就可求出对应的x的值.
解答:解:(1)过点B作BH⊥OA于H,如图1,
∵四边形OABC是直角梯形,∴∠BCO=90°.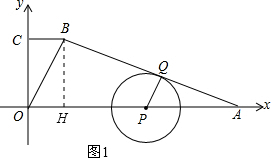
∵C(0,8),即OC=8,OB=10,
∴BC=6.
∵∠BCO=∠COH=∠BHO=90°,
∴四边形BCOH是矩形.
∴BH=OC=8,OH=BC=6.
∵A(21,0),即OA=21,∴AH=21-6=15.
在Rt△BHA中,
AB=
=
=17.
∴S△OAB=
OA•BH=
×21×8=84.
(2)过点B作BH⊥OA于H,过点B作BS⊥AB交OA于S,如图2,
∵⊙P与AB相切于点Q,∴PQ⊥AB.
∴∠AQP=∠BHA=90°.
∵∠QAP=∠HAB,
∴△PQA∽△BHA.
∴
=
.
∴
=
.
∴AP=17x.
∵BS⊥AB,BH⊥OA,
∴∠BHA=∠SBA=90°.
∵∠BAH=∠SAB,
∴△BHA∽△SBA.
∴
=
.
∴
=
.
∴AS=
.
∵⊙P始终与AB边相切,∴0<AP≤AS.
∵点P在线段AO上运动,∴0≤AP≤AO.
∴0<AP≤AS.
∴0<17x≤
.
∴0<x≤
.
∴AP=17x,0<x≤
.
(3)①若点O在⊙P上,则OP=PQ=8x.
∴8x=21-17x.
解得:x=
.
②若⊙O的半径为16,且⊙P与⊙O相切,
Ⅰ.当⊙P与⊙O外切时,
则有OP=8x+16=21-17x.
解得:x=
.
Ⅱ.当⊙P与⊙O内切时,
则有OP=
=21-17x.
x=
或x=
.
∵0<x≤
,
∴x=
.
综上所述:满足要求的x的值为
或
.
③若⊙P与AB、OB都相切,
设⊙P与AB、OB分别相切于点F、E,连接PF、PE、BP,如图3.
则有PF⊥AB,PE⊥OB.
∵S△OAB=S△ABP+S△OBP,
∴84=
×17×8x+
×10×8x.
解得:x=
.
∵四边形OABC是直角梯形,∴∠BCO=90°.

∵C(0,8),即OC=8,OB=10,
∴BC=6.
∵∠BCO=∠COH=∠BHO=90°,
∴四边形BCOH是矩形.
∴BH=OC=8,OH=BC=6.
∵A(21,0),即OA=21,∴AH=21-6=15.
在Rt△BHA中,
AB=
| BH2+AH2 |
| 82+152 |
∴S△OAB=
| 1 |
| 2 |
| 1 |
| 2 |
(2)过点B作BH⊥OA于H,过点B作BS⊥AB交OA于S,如图2,
∵⊙P与AB相切于点Q,∴PQ⊥AB.
∴∠AQP=∠BHA=90°.
∵∠QAP=∠HAB,

∴△PQA∽△BHA.
∴
| PQ |
| BH |
| AP |
| AB |
∴
| 8x |
| 8 |
| AP |
| 17 |
∴AP=17x.
∵BS⊥AB,BH⊥OA,
∴∠BHA=∠SBA=90°.
∵∠BAH=∠SAB,
∴△BHA∽△SBA.
∴
| AB |
| AS |
| AH |
| AB |
∴
| 17 |
| AS |
| 15 |
| 17 |
∴AS=
| 289 |
| 15 |
∵⊙P始终与AB边相切,∴0<AP≤AS.
∵点P在线段AO上运动,∴0≤AP≤AO.
∴0<AP≤AS.
∴0<17x≤
| 289 |
| 15 |
∴0<x≤
| 17 |
| 15 |
∴AP=17x,0<x≤
| 17 |
| 15 |
(3)①若点O在⊙P上,则OP=PQ=8x.
∴8x=21-17x.
解得:x=
| 21 |
| 25 |
②若⊙O的半径为16,且⊙P与⊙O相切,
Ⅰ.当⊙P与⊙O外切时,
则有OP=8x+16=21-17x.
解得:x=
| 1 |
| 5 |
Ⅱ.当⊙P与⊙O内切时,
则有OP=
|
x=
| 5 |
| 9 |
| 37 |
| 25 |
∵0<x≤
| 17 |
| 15 |
∴x=
| 5 |
| 9 |

综上所述:满足要求的x的值为
| 1 |
| 5 |
| 5 |
| 9 |
③若⊙P与AB、OB都相切,
设⊙P与AB、OB分别相切于点F、E,连接PF、PE、BP,如图3.
则有PF⊥AB,PE⊥OB.
∵S△OAB=S△ABP+S△OBP,
∴84=
| 1 |
| 2 |
| 1 |
| 2 |
解得:x=
| 7 |
| 9 |
点评:本题考查了切线的性质、相切两圆的性质、矩形的判定与性质、相似三角形的判定与性质、勾股定理等知识,还考查了分类讨论的思想.而解题中所采用的面积法是求垂线段长度常用的一种方法,应掌握它.本题是一道易错题,容易把“⊙P始终与AB边相切”与“⊙P始终与直线AB相切”相混淆,需注意.

练习册系列答案
相关题目
 如图,在梯形ABCD中,AD∥BC,∠DCB=60°,BD⊥CD,BC=6,AD=2.求AB长.
如图,在梯形ABCD中,AD∥BC,∠DCB=60°,BD⊥CD,BC=6,AD=2.求AB长. 实数a在数轴上的位置如图所示,则
实数a在数轴上的位置如图所示,则