题目内容
如图1,在矩形ABCD中,AB=4cm,AD=6cm,以AB为直径作圆⊙O,动点P、Q分别同时从A、C出发,点P以1cm/s的速度向D移动,点Q以2cm/s的速度向B移动,点Q移动到B点时停止,点P也随之停止.设运动时间为ts,求:
(1)当PQ⊥BC时,求t的值;
(2)如图2,当PQ与⊙O相切时,求t的值;
(3)连接DQ,当△PDQ为等腰三角形时,直接写出t的所有值.
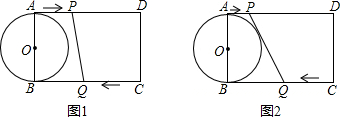
(1)当PQ⊥BC时,求t的值;
(2)如图2,当PQ与⊙O相切时,求t的值;
(3)连接DQ,当△PDQ为等腰三角形时,直接写出t的所有值.

考点:圆的综合题
专题:
分析:(1)由AP+CQ=6时得出t的值即可.
(2)设运动时间为ts,由AB2+(AP-QB)2=(AP+QB)2,列出t方程求解.
(3)分三种情况讨论:①当QD=PD时,②当DQ=AQ时,③当AQ=PD时,分别列出方程求解即可.
(2)设运动时间为ts,由AB2+(AP-QB)2=(AP+QB)2,列出t方程求解.
(3)分三种情况讨论:①当QD=PD时,②当DQ=AQ时,③当AQ=PD时,分别列出方程求解即可.
解答:解:(1)∵PQ⊥BC,
∴AP+CQ=6,
设运动时间为ts,由有AP=t,CQ=2t,
∴t+2t=6,解得t=2;
(2)如图1,PG与圆相切于点F,设运动时间为ts,

∵PA与PF是⊙O的切线,QB与QF是⊙O的切线,
∴AP=PF,QB=QF,
∴AP=PF=t,QB=QF=6-2t,
∴AB2+(AP-QB)2=(AP+QB)2,即42+(3t-6)2=(6-t)2,
解得t=1或2.
∴PQ与⊙O相切时,求t的值为1或2;
(3)①当QD=PD时,
=6-t,解得t=
-2或-
-2(舍去).
②当DQ=PQ时,
=
,解得t=
或6(舍去),
③当PQ=PD时,
=6-t,解得t=1或2.
综上所述t=
-2或
或1或2时,△PDQ为等腰三角形.
∴AP+CQ=6,
设运动时间为ts,由有AP=t,CQ=2t,
∴t+2t=6,解得t=2;
(2)如图1,PG与圆相切于点F,设运动时间为ts,

∵PA与PF是⊙O的切线,QB与QF是⊙O的切线,
∴AP=PF,QB=QF,
∴AP=PF=t,QB=QF=6-2t,
∴AB2+(AP-QB)2=(AP+QB)2,即42+(3t-6)2=(6-t)2,
解得t=1或2.
∴PQ与⊙O相切时,求t的值为1或2;
(3)①当QD=PD时,
| (2t)2+42 |
4
| ||
| 3 |
4
| ||
| 3 |
②当DQ=PQ时,
| (2t)2+42 |
| (6-2t-t)2+42 |
| 6 |
| 5 |
③当PQ=PD时,
| (6-2t-t)2+42 |
综上所述t=
4
| ||
| 3 |
| 6 |
| 5 |
点评:本题主要考查了圆的综合题,涉及圆的知识,方程及等腰三角形的性质.难点是第三小问,解题的关键是分三种情况讨论.

练习册系列答案
相关题目

 如图,B为线段AD上一点,△ABC和△BDE都是等边三角形,连接CE并延长交AD的延长线于点F,△ABC的外接圆⊙O交CF于点P.
如图,B为线段AD上一点,△ABC和△BDE都是等边三角形,连接CE并延长交AD的延长线于点F,△ABC的外接圆⊙O交CF于点P.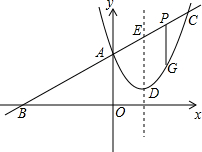 如图,已知二次函数图象的顶点坐标为D(1,1),直线y=kx+m的图象与该二次函数的图象交于A、C两点,且A(0,2),直线与x轴的交点为B,满足
如图,已知二次函数图象的顶点坐标为D(1,1),直线y=kx+m的图象与该二次函数的图象交于A、C两点,且A(0,2),直线与x轴的交点为B,满足 一次函数y=kx+k过点(1,4),且分别与x轴、y轴交于A、B点,点P(a,0)在x轴正半轴上运动,点Q(0,b)在y轴正半轴上运动,且PQ⊥AB.
一次函数y=kx+k过点(1,4),且分别与x轴、y轴交于A、B点,点P(a,0)在x轴正半轴上运动,点Q(0,b)在y轴正半轴上运动,且PQ⊥AB.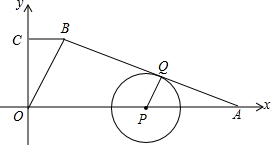 如图,在平面直角坐标系中,已知直角梯形OABC,BC∥OA,A(21,0),C(0,8),OB=10,点P在线段AO上运动,以点P为圆心作⊙P,使⊙P始终与AB边相切,切点为Q,设⊙P的半径为8x,
如图,在平面直角坐标系中,已知直角梯形OABC,BC∥OA,A(21,0),C(0,8),OB=10,点P在线段AO上运动,以点P为圆心作⊙P,使⊙P始终与AB边相切,切点为Q,设⊙P的半径为8x,