题目内容
某工厂在生产过程中要消耗大量电能,消耗每千度电产生利润与电价是一次函数关系,经过测算,工厂每千度电产生利润y(元/千度))与电价x(元/千度)的函数图象如图:
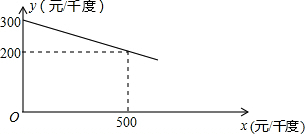
(1)当电价为600元/千度时,工厂消耗每千度电产生利润是多少?
(2)为了实现节能减排目标,有关部门规定,该厂电价x(元/千度)与每天用电量m(千度)的函数关系为x=5m+600,且该工厂每天用电量不超过60千度,为了获得最大利润,工厂每天应安排使用多少度电?工厂每天消耗电产生利润最大是多少元?

(1)当电价为600元/千度时,工厂消耗每千度电产生利润是多少?
(2)为了实现节能减排目标,有关部门规定,该厂电价x(元/千度)与每天用电量m(千度)的函数关系为x=5m+600,且该工厂每天用电量不超过60千度,为了获得最大利润,工厂每天应安排使用多少度电?工厂每天消耗电产生利润最大是多少元?
考点:二次函数的应用,一次函数的应用
专题:
分析:(1)设y=kx+b(k≠0),利用待定系数法求一次函数解析式解答即可;
(2)根据利润=每天的用电量×每千度电产生利润y,然后整理得到W与m的关系式,再根据二次函数的最值问题解答.
(2)根据利润=每天的用电量×每千度电产生利润y,然后整理得到W与m的关系式,再根据二次函数的最值问题解答.
解答:解:(1)设工厂每千度电产生利润y(元/千度)与电价x(元/千度)的函数解析式为:y=kx+b,
∵该函数图象过点(0,300),(500,200),
∴
,
解得
.
所以y=-0.2x+300(x≥0),
当电价x=600元/千度时,该工厂消耗每千度电产生利润y=-0.2×600+300=180(元/千度);
(2)设工厂每天消耗电产生利润为w元,由题意得:
w=my=m(-0.2x+300)
=m[-0.2(5m+600)+300]
=-m2+180m
=-(m-90)2+8100,
在m≤90时,w随m的增大而最大,
由题意,m≤60,
∴当m=60时,w最大=-(60-90)2+8100=7200,
即当工厂每天消耗60千度电时,工厂每天消耗电产生利润为最大,最大利润为7200元.
∵该函数图象过点(0,300),(500,200),
∴
|
解得
|
所以y=-0.2x+300(x≥0),
当电价x=600元/千度时,该工厂消耗每千度电产生利润y=-0.2×600+300=180(元/千度);
(2)设工厂每天消耗电产生利润为w元,由题意得:
w=my=m(-0.2x+300)
=m[-0.2(5m+600)+300]
=-m2+180m
=-(m-90)2+8100,
在m≤90时,w随m的增大而最大,
由题意,m≤60,
∴当m=60时,w最大=-(60-90)2+8100=7200,
即当工厂每天消耗60千度电时,工厂每天消耗电产生利润为最大,最大利润为7200元.
点评:本题考查了二次函数的应用,主要利用了待定系数法求一次函数解析式,利用二次函数的增减性求最值问题,难点在于(2)列出关于利利润的表达式.

练习册系列答案
相关题目

 如图,B为线段AD上一点,△ABC和△BDE都是等边三角形,连接CE并延长交AD的延长线于点F,△ABC的外接圆⊙O交CF于点P.
如图,B为线段AD上一点,△ABC和△BDE都是等边三角形,连接CE并延长交AD的延长线于点F,△ABC的外接圆⊙O交CF于点P.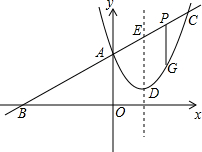 如图,已知二次函数图象的顶点坐标为D(1,1),直线y=kx+m的图象与该二次函数的图象交于A、C两点,且A(0,2),直线与x轴的交点为B,满足
如图,已知二次函数图象的顶点坐标为D(1,1),直线y=kx+m的图象与该二次函数的图象交于A、C两点,且A(0,2),直线与x轴的交点为B,满足 一次函数y=kx+k过点(1,4),且分别与x轴、y轴交于A、B点,点P(a,0)在x轴正半轴上运动,点Q(0,b)在y轴正半轴上运动,且PQ⊥AB.
一次函数y=kx+k过点(1,4),且分别与x轴、y轴交于A、B点,点P(a,0)在x轴正半轴上运动,点Q(0,b)在y轴正半轴上运动,且PQ⊥AB.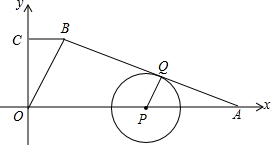 如图,在平面直角坐标系中,已知直角梯形OABC,BC∥OA,A(21,0),C(0,8),OB=10,点P在线段AO上运动,以点P为圆心作⊙P,使⊙P始终与AB边相切,切点为Q,设⊙P的半径为8x,
如图,在平面直角坐标系中,已知直角梯形OABC,BC∥OA,A(21,0),C(0,8),OB=10,点P在线段AO上运动,以点P为圆心作⊙P,使⊙P始终与AB边相切,切点为Q,设⊙P的半径为8x,